题目内容
已知函数f(x)=xln x.
(1)求函数f(x)的单调区间;
(2)k为正常数,设g(x)=f(x)+f(k-x),求函数g(x)的最小值;
(3)若a>0,b>0证明:f(a)+(a+b)ln2≥f(a+b)-f(b)
解:(1)f′(x)=ln x+1,f′(x)>0,得x> ;
;
f′(x)<0,得0<x< ,
,
∴f(x)的单调递增区间是( ,+∞),单调递减区间是(0,
,+∞),单调递减区间是(0, ).…(3分)
).…(3分)
(2)∵g(x)=f(x)+f(k-x)=x ln x+(k-x)ln(k-x),定义域是(0,k)
∴g′(x)=ln x+1-[ln (k-x)+1]=ln …(5分)
…(5分)
由g′(x>0,得 <x<k,由g′(x<0,得0<x<
<x<k,由g′(x<0,得0<x< ,
,
∴函数g(x)在(0, ) 上单调递减;在(
) 上单调递减;在( ,k)上单调递增,…(7分)
,k)上单调递增,…(7分)
故函数g(x)的最小值是:ymin=g( )=kln
)=kln .…(8分)
.…(8分)
(3)∵a>0,b>0∴在(2)中取x=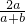 ,k=2,
,k=2,
可得f(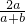 )+f(2-
)+f(2-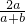 )≥2ln1 f(
)≥2ln1 f(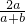 )+f(
)+f(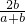 )≥0
)≥0
?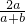 ln
ln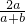 +
+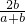 ln
ln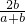 ≥0
≥0
?alna+blnb+(a+b)ln2-(a+b)ln(a+b)≥0
?f(a)+(a+b)ln2≥f(a+b)-f(b) …(12分)
分析:(1)先对函数y=f(x)进行求导,然后令导函数大于0(或小于0)求出x的范围,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,即可得到答案.
(2)构造函数g(x)=f(x)+f(k-x),(k>0),利用导函数判断出g(x)的单调性,进一步求出g(x)的最小值为 整理可得证.
整理可得证.
(3)先研究f(x)在区间[-e2,-e-1]上的单调性,再利用导数求解f(x)在区间[-e2,-e-1]上的最大值问题即可,故只要先求出函数的极值,比较极值和端点处的函数值的大小,最后确定出最大值即得.
点评:本小题主要考查函数的导数,单调性,利用导数求闭区间上函数的最值等基础知识,考查综合利用数学知识分析问题、解决问题的能力,中档题.
 ;
;f′(x)<0,得0<x<
 ,
,∴f(x)的单调递增区间是(
 ,+∞),单调递减区间是(0,
,+∞),单调递减区间是(0, ).…(3分)
).…(3分)(2)∵g(x)=f(x)+f(k-x)=x ln x+(k-x)ln(k-x),定义域是(0,k)
∴g′(x)=ln x+1-[ln (k-x)+1]=ln
 …(5分)
…(5分)由g′(x>0,得
 <x<k,由g′(x<0,得0<x<
<x<k,由g′(x<0,得0<x< ,
,∴函数g(x)在(0,
 ) 上单调递减;在(
) 上单调递减;在( ,k)上单调递增,…(7分)
,k)上单调递增,…(7分)故函数g(x)的最小值是:ymin=g(
 )=kln
)=kln .…(8分)
.…(8分)(3)∵a>0,b>0∴在(2)中取x=
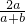 ,k=2,
,k=2,可得f(
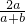 )+f(2-
)+f(2-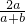 )≥2ln1 f(
)≥2ln1 f(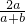 )+f(
)+f(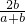 )≥0
)≥0?
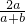 ln
ln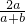 +
+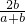 ln
ln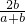 ≥0
≥0?alna+blnb+(a+b)ln2-(a+b)ln(a+b)≥0
?f(a)+(a+b)ln2≥f(a+b)-f(b) …(12分)
分析:(1)先对函数y=f(x)进行求导,然后令导函数大于0(或小于0)求出x的范围,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,即可得到答案.
(2)构造函数g(x)=f(x)+f(k-x),(k>0),利用导函数判断出g(x)的单调性,进一步求出g(x)的最小值为
 整理可得证.
整理可得证.(3)先研究f(x)在区间[-e2,-e-1]上的单调性,再利用导数求解f(x)在区间[-e2,-e-1]上的最大值问题即可,故只要先求出函数的极值,比较极值和端点处的函数值的大小,最后确定出最大值即得.
点评:本小题主要考查函数的导数,单调性,利用导数求闭区间上函数的最值等基础知识,考查综合利用数学知识分析问题、解决问题的能力,中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|