题目内容
已知椭圆 的中心在原点
的中心在原点 ,离心率
,离心率 ,右焦点为
,右焦点为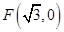 .
.
(1)求椭圆 的方程;
的方程;
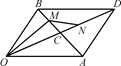
(2)设椭圆的上顶点为 ,在椭圆
,在椭圆 上是否存在点
上是否存在点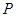 ,使得向量
,使得向量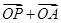 与
与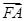 共线?若存在,求直线
共线?若存在,求直线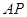
的方程;若不存在,简要说明理由.
(1)椭圆 的方程为
的方程为 ;(2)存在,且直线
;(2)存在,且直线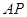 的方程为
的方程为 或
或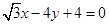 .
.
解析试题分析:(1)先设椭圆 的方程
的方程 ,利用离心率以及焦点坐标求出
,利用离心率以及焦点坐标求出 、
、 、
、 的值,进而确定椭圆
的值,进而确定椭圆 的方程;(2)先设点
的方程;(2)先设点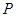 的坐标为
的坐标为 ,利用向量
,利用向量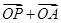 与
与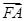 共线这一条件得到点
共线这一条件得到点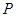 的坐标之间所满足的关系,并代入椭圆
的坐标之间所满足的关系,并代入椭圆 的方程解出点
的方程解出点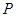 的坐标,然后确定直线
的坐标,然后确定直线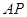 的方程.
的方程.
试题解析:(1)设椭圆 的方程为
的方程为 , 1分
, 1分
离心率 ,右焦点为
,右焦点为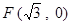 ,
,
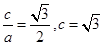 ,
,
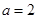 ,
, 3分
3分
故椭圆 的方程为
的方程为 . 4分
. 4分
(2)假设椭圆 上存在点
上存在点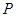 (
(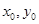 ),使得向量
),使得向量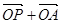 与
与 共线, 5分
共线, 5分
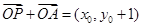 ,
, ,
,
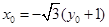 (1) 6分
(1) 6分
又 点
点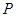 (
(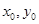 )在椭圆
)在椭圆 上,
上,
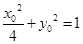 (2) 8分
(2) 8分
由(1)、(2)组成方程组解得: ,或
,或 , 11分
, 11分
当点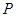 的坐标为
的坐标为 时,直线
时,直线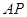 的方程为
的方程为 ,
,
当点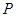 的坐标为
的坐标为 时,直线
时,直线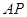 的方程为
的方程为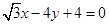 ,
,
故直线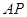 的方程为
的方程为 或
或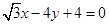 . 14分
. 14分
考点:1.椭圆的方程;2.平面向量共线;3.直线的方程

练习册系列答案
相关题目
已知平面向量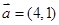 ,
,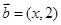 ,且
,且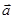 与
与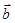 平行,则
平行,则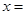 ( ).
( ).
A.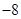 | B.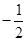 | C.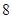 | D. |
已知向量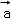 =(2,1),
=(2,1),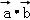 =10,|
=10,|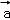 +
+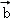 |=
|=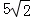 ,则|
,则|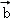 |=( )
|=( )
A.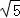 | B.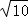 | C.5 | D.25 |
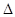 OAB中,点A是BC的中点,点D是将向量
OAB中,点A是BC的中点,点D是将向量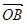 分为2:1的一个分点,DC和OA交于点E.设
分为2:1的一个分点,DC和OA交于点E.设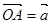 ,
,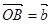
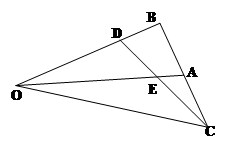
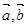 表示
表示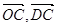 ;
;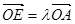 ,求实数
,求实数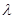 的值.
的值.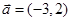 ,
,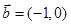 ,设
,设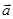 与
与 的夹角为
的夹角为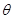 .
.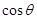 ;
;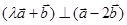 ,求
,求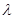 的值.
的值.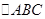 中,
中,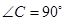 ,点E是BC上一点,且满足:
,点E是BC上一点,且满足: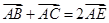 ,以A为圆心,AC的长为半径作圆交AB于D,交AE于F.若
,以A为圆心,AC的长为半径作圆交AB于D,交AE于F.若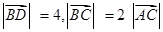 ,求
,求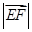 的值.
的值. 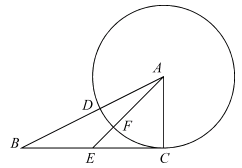
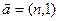 与
与 共线且方向相同,则n=
共线且方向相同,则n=  是四边形
是四边形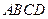 内一点,满足
内一点,满足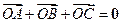 ,若
,若 ,则
,则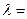 ▲ .
▲ .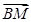 =
=
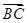 ,
,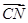 =
=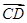 ,
, =a,
=a, =b,用a、b表示
=b,用a、b表示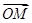 、
、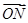 、
、 .
.