题目内容
设函数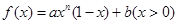 ,
,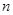 为正整数,
为正整数, 为常数,曲线
为常数,曲线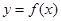 在
在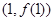 处的切线方程为
处的切线方程为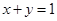 。
。
(1)求 的值; (2)求函数
的值; (2)求函数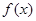 的最大值; (3)证明:
的最大值; (3)证明: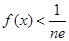 。
。
【答案】
(1)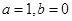 (2)
(2)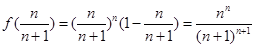
(3)见解析
【解析】(1)因为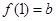 ,由点
,由点 在
在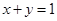 上,可得
上,可得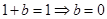
因为 ,所以
,所以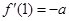
又因为切线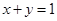 的斜率为
的斜率为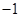 ,所以
,所以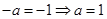 ,所以
,所以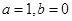
(2)由(1)可知,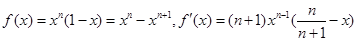
令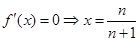 ,即
,即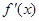 在
在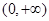 上有唯一的零点
上有唯一的零点 。
。
在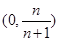 上,
上,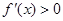 ,故
,故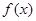 单调递增;而在
单调递增;而在 上,
上,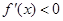 ,
,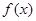 单调递减,故
单调递减,故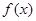 在
在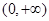 的最大值为
的最大值为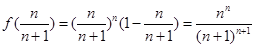 。
。
(3)令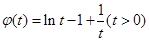 ,则
,则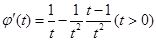
在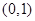 上,
上,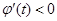 ,故
,故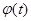 单调递减,而在
单调递减,而在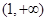 上,
上,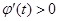 ,
,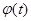 单调递增,
单调递增,
故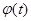 在
在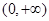 上的最小值为
上的最小值为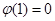 ,所以
,所以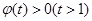 即
即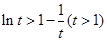 ,令
,令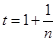 ,得
,得 ,即
,即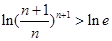 所以
所以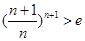 ,即
,即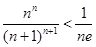 由(2)知,
由(2)知, ,故所证不等式成立。
,故所证不等式成立。
【点评】本题考查多项式函数的求导,导数的几何意义,导数判断函数的单调性,求解函数的最值以及证明不等式等的综合应用.考查转化与划归,分类讨论的数学思想以及运算求解的能力. 导数的几何意义一般用来求曲线的切线方程,导数的应用一般用来求解函数的极值,最值,证明不等式等. 来年需注意应用导数判断函数的极值以及求解极值,最值等;另外,要注意含有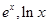 等的函数求导的运算及其应用考查
等的函数求导的运算及其应用考查

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
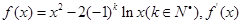 表示
表示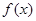 导函数。
导函数。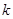 为奇数时,设
为奇数时,设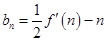 ,数列
,数列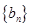 的前
的前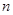 项和为
项和为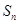 ,证明不等式
,证明不等式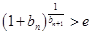 对一切正整数
对一切正整数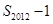 与
与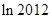 的大小.
的大小. 为正整数,
为正整数,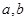 为常数.曲线
为常数.曲线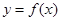 在点
在点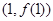 处的切线方程为
处的切线方程为 .
. 的最大值;
的最大值;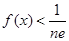 .
.