题目内容
设函数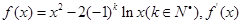 表示
表示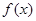 导函数。
导函数。
(1)求函数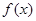 的单调递增区间;
的单调递增区间;
(2)当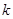 为奇数时,设
为奇数时,设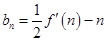 ,数列
,数列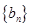 的前
的前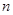 项和为
项和为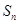 ,证明不等式
,证明不等式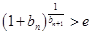 对一切正整数
对一切正整数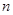 均成立,并比较
均成立,并比较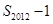 与
与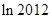 的大小.
的大小.
【答案】
(1) 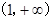 (2)
(2)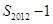 <
<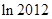
【解析】
试题分析:(I)定义域为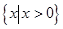 ,
,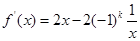
当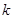 为奇数时,
为奇数时,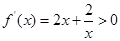 恒成立,
恒成立,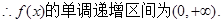
当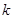 为偶数时,
为偶数时,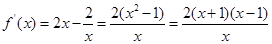 ,
,
又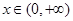 ,
,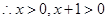 ,
,
由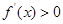 ,
,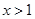 ,
,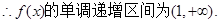
(2)当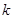 为奇数时,
为奇数时,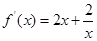
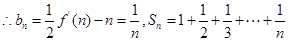
要证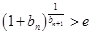 ,即证
,即证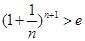 ,两边取对数,即证
,两边取对数,即证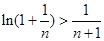
设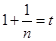 ,则
,则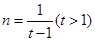 ,
,
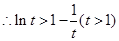 ,构造函数
,构造函数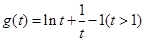 ,
,
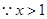 ,
, ,
,
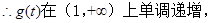
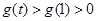 ,
,
即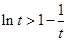 ,
,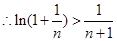 ,即
,即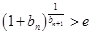 .
.
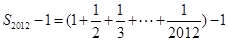
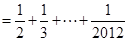
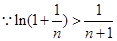 ,
,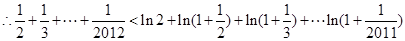
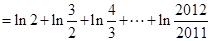
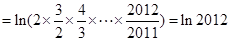
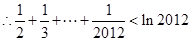
考点:利用导数研究函数的单调性;不等式比较大小;数列递推式.
点评:本小题主要考查等差关系的确定、利用导数研究函数的单调性、证明不等式等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
相关题目
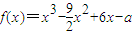 .
.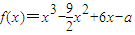 .
.