题目内容
若存在正数x使2x(x－a)<1成立，则a的取值范围是________．
(－1，＋∞)
因为2x(x－a)<1，所以a>x－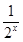
，令f(x)＝x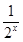－，所以f′(x)＝1＋2－xln2>0，所以f(x)在(0，＋∞)上单调递增，所以f(x)>f(0)＝0－1＝－1，所以a的取值范围是(－1，＋∞)
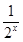，令f(x)＝x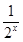－，所以f′(x)＝1＋2－xln2>0，所以f(x)在(0，＋∞)上单调递增，所以f(x)>f(0)＝0－1＝－1，所以a的取值范围是(－1，＋∞)
练习册系列答案
阅读快车系列答案
相关题目
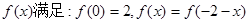，它的导函数的图象与直线
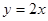平行.
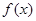的解析式；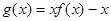
的图象与直线
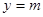有三个公共点，求m的取值范围．
－
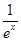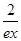成立．
的图象如图所示（其中
是函数
的导函数）．下面四个图象中，
的图象大致是（ ）
在
上是单调函数,则实数
的取值范围是（ ）
x2－mlnx＋(m－1)x，当m≤0时，试讨论函数f(x)的单调性；
