题目内容
 (2013•海淀区一模)在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=
(2013•海淀区一模)在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=| 2 |
(Ⅰ)求证:BD⊥PC;
(Ⅱ)求证:MN∥平面PDC;
(Ⅲ)求二面角A-PC-B的余弦值.
分析:(Ⅰ)由正三角形的性质可得BD⊥AC,利用线面垂直的性质可知PA⊥BD,再利用线面垂直的判定定理即可证明BD⊥PC;
(Ⅱ)利用已知条件分别求出BM、MD、PB,得到
=
,即可得到MN∥PD,再利用线面平行的判定定理即可证明;
(Ⅲ)通过建立空间直角坐标系,利用两个平面的法向量的夹角即可得到二面角的平面角.
(Ⅱ)利用已知条件分别求出BM、MD、PB,得到
| BM |
| MD |
| BN |
| NP |
(Ⅲ)通过建立空间直角坐标系,利用两个平面的法向量的夹角即可得到二面角的平面角.
解答:证明:(I)∵△ABC是正三角形,M是AC中点,
∴BM⊥AC,即BD⊥AC.
又∵PA⊥平面ABCD,∴PA⊥BD.
又PA∩AC=A,∴BD⊥平面PAC.
∴BD⊥PC.
(Ⅱ)在正△ABC中,BM=2
.
在△ACD中,∵M为AC中点,DM⊥AC,∴AD=CD.
∠ADC=120°,∴DM=
,
∴
=
.
在等腰直角△PAB中,PA=AB=4,PB=4
,
∴
=
,
∴
=
,
∴MN∥PD.
又MN?平面PDC,PD?平面PDC,
∴MN∥平面PDC.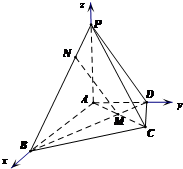
(Ⅲ)∵∠BAD=∠BAC+∠CAD=90°,
∴AB⊥AD,分别以AB,AD,AP为x轴,y轴,z轴建立如图的空间直角坐标系,
∴B(4,0,0),C(2,2
,0),D(0,
,0),P(0,0,4).
由(Ⅱ)可知,
=(4,-
,0)为平面PAC的法向量.
=(2,2
,-4),
=(4,0,-4).
设平面PBC的一个法向量为
=(x,y,z),
则
,即
,
令z=3,得x=3,y=
,则平面PBC的一个法向量为
=(3,
,3),
设二面角A-PC-B的大小为θ,则cosθ=
=
.
所以二面角A-PC-B余弦值为
.
∴BM⊥AC,即BD⊥AC.
又∵PA⊥平面ABCD,∴PA⊥BD.
又PA∩AC=A,∴BD⊥平面PAC.
∴BD⊥PC.
(Ⅱ)在正△ABC中,BM=2
| 3 |
在△ACD中,∵M为AC中点,DM⊥AC,∴AD=CD.
∠ADC=120°,∴DM=
2
| ||
| 3 |
∴
| BM |
| MD |
| 3 |
| 1 |
在等腰直角△PAB中,PA=AB=4,PB=4
| 2 |
∴
| BN |
| NP |
| 3 |
| 1 |
∴
| BN |
| NP |
| BM |
| MD |
∴MN∥PD.
又MN?平面PDC,PD?平面PDC,
∴MN∥平面PDC.

(Ⅲ)∵∠BAD=∠BAC+∠CAD=90°,
∴AB⊥AD,分别以AB,AD,AP为x轴,y轴,z轴建立如图的空间直角坐标系,
∴B(4,0,0),C(2,2
| 3 |
4
| ||
| 3 |
由(Ⅱ)可知,
| DB |
4
| ||
| 3 |
| PC |
| 3 |
| PB |
设平面PBC的一个法向量为
| n |
则
|
|
令z=3,得x=3,y=
| 3 |
| n |
| 3 |
设二面角A-PC-B的大小为θ,则cosθ=
| ||||
|
|
| ||
| 7 |
所以二面角A-PC-B余弦值为
| ||
| 7 |
点评:熟练掌握正三角形的性质、线面垂直的判定与性质定理、平行线分线段成比例在三角形中的逆定理应用、通过建立空间直角坐标系并利用两个平面的法向量的夹角得到二面角的平面角是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 (2013•海淀区一模)在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又∠CAD=30°,PA=AB=4,点N在线段PB上,且
(2013•海淀区一模)在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又∠CAD=30°,PA=AB=4,点N在线段PB上,且