题目内容
(本小题满分12分)在 ABC中,内角A,B,C的对边分别为a,b,c.已知cosA=
ABC中,内角A,B,C的对边分别为a,b,c.已知cosA= ,sinB=
,sinB= cosC.
cosC.
(Ⅰ)求tanC的值;
(Ⅱ)若a= ,求
,求 ABC的面积
ABC的面积
【答案】
(Ⅰ)  ;(Ⅱ)
;(Ⅱ)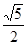 。
。
【解析】
试题分析:(1)因为cosA=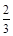 >0,, 所以sinA=
>0,, 所以sinA=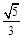
又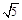 cosC=sinB=sin(A+C)=sinAcosC+sinCcosA
cosC=sinB=sin(A+C)=sinAcosC+sinCcosA
=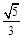 cosC+
cosC+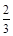 sinC.
sinC.
整理得:tanC=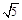 .
.
(Ⅱ)由图辅助三角形知:sinC=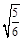 .又由正弦定理知:
.又由正弦定理知: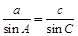 ,
,
故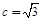 . (1)
. (1)
对角A运用余弦定理:cosA=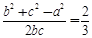 . (2)
. (2)
解(1) (2)得: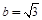 或 b=
或 b=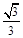 (舍去).
(舍去).
∴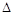 ABC的面积为:S=
ABC的面积为:S=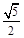 .
.
考点:本题考查正弦定理、余弦定理、三角形的面积公式、和三角形内的隐含条件。
点评:做三角函数的有关题目时,要注意三角形内隐含条件的应用。常用的三角形内的隐含条件有:① ,
, ,
,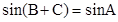 ;②
;②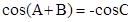 ,
,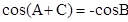 ,
,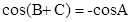 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目