题目内容
若已知f(a)<0,f(b)>0,则下列说法中正确的是
- A.f(x)在(a,b)上必有且只有一个零点
- B.f(x)在(a,b)上必有正奇数个零点
- C.f(x)在(a,b)上必有正偶数个零点
- D.f(x)在(a,b)上可能有正偶数个零点,也可能有正奇数个零点,还可能没有零点
D
分析:本题为选择题,可以采用排除法,因为已知给定条件较少,不能确定f(x)在(a,b)上的零点的个数,也就是f(x)图象与x轴的交点的个数,通过画简图,很容易判断A,B,C都不正确.
解答:若f(x)不连续则可能没有零点,则A不正确;若f(x)在该区间有二重零点则可能有正偶数个零点,
同样也有可能有正奇数个零点.故B和C不正确;故应选D.
点评:本题主要考查函数的零点,属于函数的基本知识.
分析:本题为选择题,可以采用排除法,因为已知给定条件较少,不能确定f(x)在(a,b)上的零点的个数,也就是f(x)图象与x轴的交点的个数,通过画简图,很容易判断A,B,C都不正确.
解答:若f(x)不连续则可能没有零点,则A不正确;若f(x)在该区间有二重零点则可能有正偶数个零点,
同样也有可能有正奇数个零点.故B和C不正确;故应选D.
点评:本题主要考查函数的零点,属于函数的基本知识.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
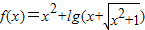 有以下四个结论:
有以下四个结论: