题目内容
（2012•大连二模）△ABC中，已知AB=2
，BC=3
，AC=7．D是边AC上一点，将△ABD沿BD折起，得到三棱锥A-BCD．若该三棱锥的顶点A在底面BCD的射影M在线段BC上，设BM=x，则x的取值范围为（ ）
| 7 |
| 7 |
分析：根据题意可得：折叠前在图1中，AM⊥BD，垂足为N．设图1中A点在BC上的射影为M1，运动点D并加以观察，可得
当D点与C点无限接近时，点M与点M1无限接近，所以BM＞BM1．在图2中根据斜边大于直角边，可得BM＜AB，所以BM1＜BM＜AB．最后在△ABC中，利用余弦定理算出∠ABC=60°，然后在Rt△AM1B中算出BM1=
，可得答案．
当D点与C点无限接近时，点M与点M1无限接近，所以BM＞BM1．在图2中根据斜边大于直角边，可得BM＜AB，所以BM1＜BM＜AB．最后在△ABC中，利用余弦定理算出∠ABC=60°，然后在Rt△AM1B中算出BM1=
| 7 |
解答：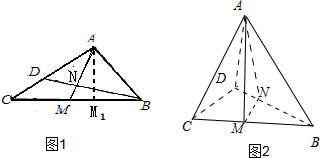
解：根据题意，可得
∵将△ABD沿BD折起，得到三棱锥A-BCD，且点A在底面BCD的射影M在线段BC上，
∴在图2中，AM⊥平面BCD，MN、AN都与BD垂直
因此，折叠前在图1中，AM⊥BD，垂足为N．
在图1中过A作AM1⊥BC于M1，运动点D可得当D点与C点无限接近时，折痕BD接近BC，此时M与点M1无限接近；
在图2中，由于AB是Rt△ABM的斜边，BM是直角边，所以BM＜AB．
由此可得：BM1＜BM＜AB，
∵△ABC中，AB=2
，BC=3
，AC=7，
∴cos∠ABC=
=
，可得∠ABC=60°，
由此可得Rt△AM1B中，BM1=ABcos60°=
，
∴
＜BM＜2
，由BM=x可得x的取值范围为（
，2
）．
故选：C
解：根据题意，可得∵将△ABD沿BD折起，得到三棱锥A-BCD，且点A在底面BCD的射影M在线段BC上，
∴在图2中，AM⊥平面BCD，MN、AN都与BD垂直
因此，折叠前在图1中，AM⊥BD，垂足为N．
在图1中过A作AM1⊥BC于M1，运动点D可得当D点与C点无限接近时，折痕BD接近BC，此时M与点M1无限接近；
在图2中，由于AB是Rt△ABM的斜边，BM是直角边，所以BM＜AB．
由此可得：BM1＜BM＜AB，
∵△ABC中，AB=2
| 7 |
| 7 |
∴cos∠ABC=
| 28+63-49 | ||||
2×2
|
| 1 |
| 2 |
由此可得Rt△AM1B中，BM1=ABcos60°=
| 7 |
∴
| 7 |
| 7 |
| 7 |
| 7 |
故选：C
点评：本题以平面图形的折叠为载体，求线段BM的取值范围．着重考查了空间垂直位置关系的判定与性质、余弦定理解三角形等知识，同时考查了空间想象能力与逻辑推理能力，属于中档题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
（2012•大连二模）已知程序框图如图所示，则输出的s为（ ）