题目内容
（本小题满分12分）已知数列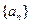
是首项为
且公比
不等于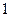
的等比数列，
是其前
项的和，
成等差数列.
（1）证明：
成等比数列；
（2）求和：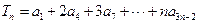
解：（1）证明 由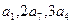
成等差数列， 得
，
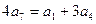即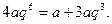 
所以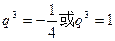
（舍去）. …（3分）
由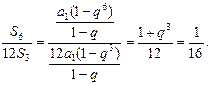 
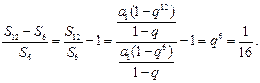
得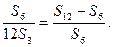 
所以成等比数列.…（6分）
（2）解：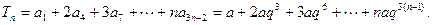
即 
…（8分）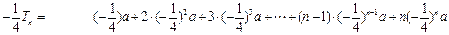
相减得：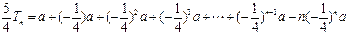
所以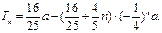 
…（12分）
解析
练习册系列答案
相关题目
题目内容
（本小题满分12分）已知数列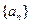是首项为且公比不等于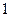的等比数列，是其前项的和，成等差数列.
（1）证明：成等比数列；
（2）求和：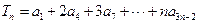
解：（1）证明 由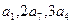成等差数列， 得，
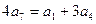即 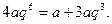所以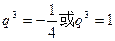（舍去）. …（3分）
由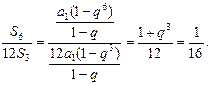
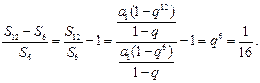
得 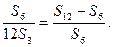所以成等比数列.…（6分）
（2）解：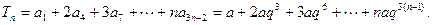
即 …（8分）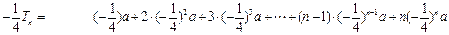
相减得：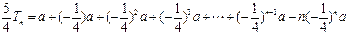
所以 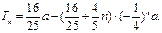…（12分）
解析
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
