Question

已知函数f(x)=ax+

b

x

（b≠0）的图象是以直线y=ax和y轴为渐近线的双曲线．则由函数f(x)=

3 x

3

+

2 3

x

表示的双曲线的实轴长等于

 

．

Answer 1

分析：先根据题意画出图形，如图，由函数f(x)=

3 x

3

+

2 3

x

表示的双曲线的是以直线y=

3

3

x和y轴为渐近线的双曲线．
得出即双曲线的实轴所在的直线的方程，通过解方程组：

y= 3 x y= 3 x 3 + 2 3 x

求得顶点坐标，从而求得双曲线的实轴长．

解答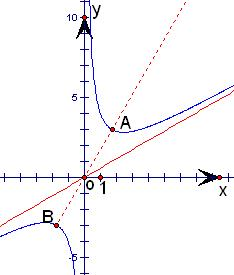：解：如图，由函数f(x)=

3 x

3

+

2 3

x

表示的双曲线的是以直线y=

3

3

x和y轴为渐近线的双曲线．
∵直线y=

3

3

x的倾斜角为：30°，
则直线OA（即双曲线的实轴所在的直线）的倾斜角为：60°，
故直线OA的方程为：y=

3

x，
由方程组：

y= 3 x y= 3 x 3 + 2 3 x

解得A（

3

，3）
∴双曲线的实轴长等于2×OA=2

3+9

=4

3

．
故答案为：4

3

．

点评：本小题主要考查双曲线的简单性质、直线与双曲线的位置关系等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．