Question

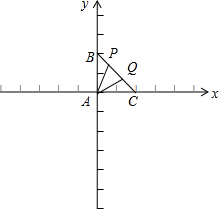
等腰直角三角形ABC中，∠BAC=90°，若P、Q为斜边BC的三等分点，则tan∠PAQ等于（　　）

• A．

  4

  3

• B．

  1

  2

• C．

  3

  3

• D．

  3

  4

Answer 1

分析：可以A点为原点，以AC所在直线为x轴，AB所在直线为y轴建立直角坐标系，求得各点的坐标，从而可得直线PA与直线AQ的斜率，利用两角差的正切公式即可求得答案．

解答：解：如图，建立直角坐标系，设AB=AC=3a，则P（a，2a），Q（2a，a），

∵tan∠PAQ=tan（∠PAC-∠QAC）
=

kAP-kAQ

1+kAP•kAQ

=

2- 1 2

1+1

=

3

4

．
故选D．

点评：本题考查直线的斜率，考查两角差的正切，考查建系与作图能力，属于中档题．