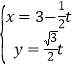题目内容
【题目】如图,已知抛物线C顶点在坐标原点,焦点F在Y轴的非负半轴上,点![]() 是抛物线上的一点.
是抛物线上的一点.

(1)求抛物线C的标准方程
(2)若点P,Q在抛物线C上,且抛物线C在点P,Q处的切线交于点S,记直线 MP,MQ的斜率分别为k1,k2,且满足![]() ,当P,Q在C上运动时,△PQS的面积是否为定值?若是,求出△PQS的面积;若不是,请说明理由.
,当P,Q在C上运动时,△PQS的面积是否为定值?若是,求出△PQS的面积;若不是,请说明理由.
【答案】(1)![]() ;(2)定值4
;(2)定值4
【解析】
(1)设出抛物线方程,将M坐标代入,计算方程,即可。(2)设出直线PQ的方程,结合![]() 得到
得到![]() ,计算S的坐标,结合点到直线距离公式,计算所求三角形高,结合直线截抛物线所得弦长,计算PQ,计算面积,即可。
,计算S的坐标,结合点到直线距离公式,计算所求三角形高,结合直线截抛物线所得弦长,计算PQ,计算面积,即可。
(1)设抛物线的方程为![]() 将M(-2,1)点坐标代入方程中,解得
将M(-2,1)点坐标代入方程中,解得![]()
(2)设![]() ,设直线PQ的方程为
,设直线PQ的方程为![]() ,代入抛物线方程
,代入抛物线方程![]() ,得到
,得到![]() ,则
,则![]() ,结合
,结合![]() ,而
,而![]()
则 ,代入,得到
,代入,得到![]() 所以
所以
![]() ,解得
,解得![]()
过P点的切线斜率为![]() ,过Q切线斜率为
,过Q切线斜率为![]() ,则PS的方程为
,则PS的方程为![]() ,QS的方程为
,QS的方程为![]() ,联解这两个方程,得到S的坐标为
,联解这两个方程,得到S的坐标为![]() ,故点S的直线PQ的距离为
,故点S的直线PQ的距离为![]() ,而PQ的长度为
,而PQ的长度为![]() ,故面积为
,故面积为
![]() ,故为定值。
,故为定值。

【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15-65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
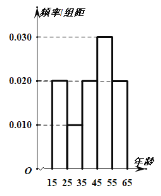
(1)由以上统计数据填2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]() .
.
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动、现从这8人中随机抽2人.记抽到45岁以上的人数为X,求随机变量X的分布列及数学期望.
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响.对近
(单位:千元)的影响.对近![]() 年的年宣传费
年的年宣传费![]() 和年销售量数据
和年销售量数据![]() 作了初步处理,得到下面的散点图及一些统计量的值.
作了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .附:对于一组数据
.附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为 ,
,![]() .
.
(1)根据散点图判断,![]() 与
与![]() 在哪一个适宜作为年销售量
在哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据1小问的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的年利润![]() 与
与![]() 的关系为
的关系为![]() .根据2小问的结果回答下列问题:
.根据2小问的结果回答下列问题:
①2年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
②3年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?