题目内容
设抛物线C:x2=2py(p>0),过它的焦点F且斜率为1的直线与抛物线C相交于A,B两点,已知|AB|=2.(1)求抛物线C的方程;
(2)已知t是一个负实数,P是直线y=t上一点,过P作直线l1与l2,使l1⊥l2,若对任意的点P,总存在这样的直线l1与l2,使l1,l2与抛物线均有公共点,求t的取值范围.
【答案】分析:(1)利用抛物线的定义,结合|AB|=2,即可求得抛物线的方程;
(2)由题意知,只需使过点P(0,t)的抛物线x2=y的切线PC的垂线PD与该抛物线有交点即可,
将直线PD的方程代入抛物线方程,得到△≥0,即可求t的取值范围.
解答:解:(1)设A(x1,y1),B(x2,y2),则|AB|=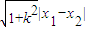 =
=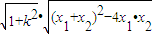
由题意知,抛物线的焦点F为(0,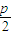 ),则直线AB的方程为
),则直线AB的方程为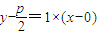 ,即为
,即为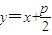 ,
,
联立抛物线方程得到 整理得x2-2px-p2=0(p>0),则
整理得x2-2px-p2=0(p>0),则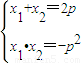
故|AB|=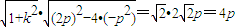 =2,解得
=2,解得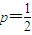
故抛物线C的方程为:x2=y;
(2)由(1)知抛物线C的方程为:x2=y,如图示,设C(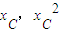 ),P(0,t),
),P(0,t),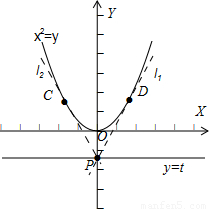
由题意知,只需使过点P(0,t)的抛物线x2=y的切线PC的垂线PD与该抛物线有交点即可,
将抛物线的方程改写为y=x2,求导得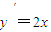
所以过点C的切线PC的斜率是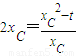 ,即
,即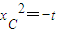
由于直线PD与切线PC垂直,故直线PD的斜率为-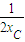
则直线PD的方程为: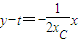 ,即是
,即是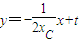
联立抛物线的方程y=x2得到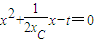
由于PD与该抛物线有交点,则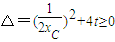 ,即
,即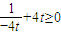 (t<0)
(t<0)
解得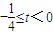 ,则t的取值范围为{t|
,则t的取值范围为{t|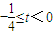 }.
}.
点评:本题考查抛物线的定义,考查直线与抛物线的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.
(2)由题意知,只需使过点P(0,t)的抛物线x2=y的切线PC的垂线PD与该抛物线有交点即可,
将直线PD的方程代入抛物线方程,得到△≥0,即可求t的取值范围.
解答:解:(1)设A(x1,y1),B(x2,y2),则|AB|=
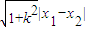 =
=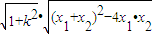
由题意知,抛物线的焦点F为(0,
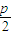 ),则直线AB的方程为
),则直线AB的方程为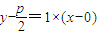 ,即为
,即为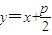 ,
,联立抛物线方程得到
 整理得x2-2px-p2=0(p>0),则
整理得x2-2px-p2=0(p>0),则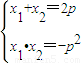
故|AB|=
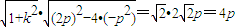 =2,解得
=2,解得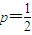
故抛物线C的方程为:x2=y;
(2)由(1)知抛物线C的方程为:x2=y,如图示,设C(
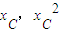 ),P(0,t),
),P(0,t),
由题意知,只需使过点P(0,t)的抛物线x2=y的切线PC的垂线PD与该抛物线有交点即可,
将抛物线的方程改写为y=x2,求导得
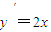
所以过点C的切线PC的斜率是
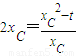 ,即
,即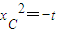
由于直线PD与切线PC垂直,故直线PD的斜率为-
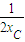
则直线PD的方程为:
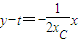 ,即是
,即是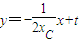
联立抛物线的方程y=x2得到
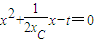
由于PD与该抛物线有交点,则
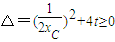 ,即
,即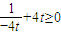 (t<0)
(t<0)解得
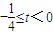 ,则t的取值范围为{t|
,则t的取值范围为{t|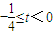 }.
}.点评:本题考查抛物线的定义,考查直线与抛物线的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
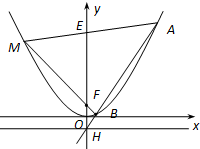 设抛物线C:x2=2py(p>0),F为焦点,抛物线C上一点P(m,3)到焦点的距离是4,抛物线C的准线l与y轴的交点为H
设抛物线C:x2=2py(p>0),F为焦点,抛物线C上一点P(m,3)到焦点的距离是4,抛物线C的准线l与y轴的交点为H