题目内容
设抛物线C:x2=2py(p>0)的焦点为F,A(x,y)(x≠0)是抛物线C上的一定点.(1)已知直线l过抛物线C的焦点F,且与C的对称轴垂直,l与C交于Q,R两点,S为C的准线上一点,若△QRS的面积为4,求p的值;
(2)过点A作倾斜角互补的两条直线AM,AN,与抛物线C的交点分别为M(x1,y1),N(x2,y2).若直线AM,AN的斜率都存在,证明:直线MN的斜率等于抛物线C在点A关于对称轴的对称点A1处的切线的斜率.
【答案】分析:(1)设出F,Q,R的坐标,求出|QR|,利用△QRS的面积为4,可求p的值;
(2)求抛物线C在点A关于对称轴的对称点A1处的切线的斜率,一种方法是设直线方程与抛物线方程联立,利用判别式为0,另一种方法是导数法;求直线MN的斜率,一种方法是设直线方程与抛物线方程联立,利用韦达定理及斜率公式,可求斜率,另一种方法是利用kAM=-kAN,确定斜率,从而可得结论.
解答:(1)解:由题设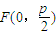 ,设
,设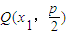 ,则
,则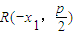 …(1分)
…(1分)
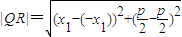 =
=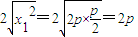 .…(2分)
.…(2分)
∴由△QRS的面积为4,得: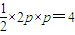 ,得:p=2.…(4分)
,得:p=2.…(4分)
(2)证明:由题意A1(-x,y)…(5分)
首先求抛物线C在点A关于对称轴的对称点A1处的切线的斜率.
解法一:设抛物线在A1处的切线的斜率为k,则其方程为y=k(x+x)+y…(6分)
联立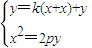 ,消去y得x2-2pkx-2pxk-2py=0
,消去y得x2-2pkx-2pxk-2py=0
将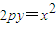 代入上式得:
代入上式得: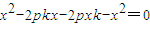 …(7分)
…(7分)
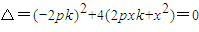 …(8分)
…(8分)
即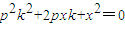 ,即
,即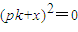 ,得
,得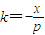 .
.
即抛物线C在点A关于对称轴的对称点A1处的切线的斜率为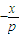 .…(9分)
.…(9分)
解法二:由x2=2py得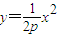 ,…(6分)
,…(6分)
∴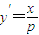 …(7分)
…(7分)
∴抛物线C在点A关于对称轴的对称点A1(-x,y)处的切线的斜率为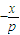 .…(9分)
.…(9分)
再求直线MN的斜率.
解法一:设直线AM的斜率为k1,则由题意直线AN的斜率为-k1.…(10分)
直线AM的方程为y-y=k1(x-x),则直线AN的方程为y-y=-k1(x-x).
联立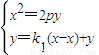 ,消去y得
,消去y得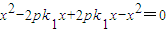 …(1)…(11分)
…(1)…(11分)
∵方程(1)有两个根x,x1,∴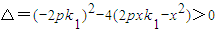
∴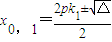 ,x+x1=2pk1,即x1=2pk1-x,同理可得x2=-2pk1-x…(12分)
,x+x1=2pk1,即x1=2pk1-x,同理可得x2=-2pk1-x…(12分)
直线MN的斜率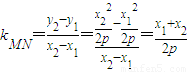 =
=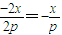 .…(13分)
.…(13分)
∴直线MN的斜率等于抛物线C在点A关于对称轴的对称点A1处的切线的斜率.…(14分)
解法二:∵kAM=-kAN…(10分)
∴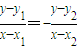 …(11分)
…(11分)
将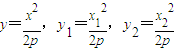 分别代入上式得:
分别代入上式得: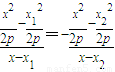 ,
,
整理得2x=x1+x2.…(12分)
∴直线MN的
斜率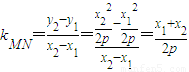 =
=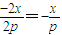 .…(13分)
.…(13分)
∴直线MN的斜率等于抛物线C在点A关于对称轴的对称点A1处的切线的斜率.…(14分)
点评:本小题主要考查直线、抛物线、对称等知识,考查数形结合、化归与转化、方程的思想方法,考查数学探究能力以及运算求解能力.
(2)求抛物线C在点A关于对称轴的对称点A1处的切线的斜率,一种方法是设直线方程与抛物线方程联立,利用判别式为0,另一种方法是导数法;求直线MN的斜率,一种方法是设直线方程与抛物线方程联立,利用韦达定理及斜率公式,可求斜率,另一种方法是利用kAM=-kAN,确定斜率,从而可得结论.
解答:(1)解:由题设
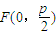 ,设
,设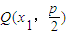 ,则
,则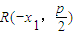 …(1分)
…(1分)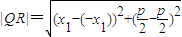 =
=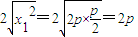 .…(2分)
.…(2分)∴由△QRS的面积为4,得:
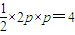 ,得:p=2.…(4分)
,得:p=2.…(4分)(2)证明:由题意A1(-x,y)…(5分)
首先求抛物线C在点A关于对称轴的对称点A1处的切线的斜率.
解法一:设抛物线在A1处的切线的斜率为k,则其方程为y=k(x+x)+y…(6分)
联立
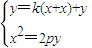 ,消去y得x2-2pkx-2pxk-2py=0
,消去y得x2-2pkx-2pxk-2py=0将
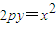 代入上式得:
代入上式得: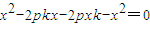 …(7分)
…(7分)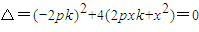 …(8分)
…(8分)即
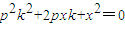 ,即
,即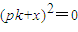 ,得
,得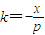 .
.即抛物线C在点A关于对称轴的对称点A1处的切线的斜率为
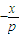 .…(9分)
.…(9分)解法二:由x2=2py得
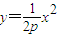 ,…(6分)
,…(6分)∴
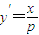 …(7分)
…(7分)∴抛物线C在点A关于对称轴的对称点A1(-x,y)处的切线的斜率为
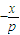 .…(9分)
.…(9分)再求直线MN的斜率.
解法一:设直线AM的斜率为k1,则由题意直线AN的斜率为-k1.…(10分)
直线AM的方程为y-y=k1(x-x),则直线AN的方程为y-y=-k1(x-x).
联立
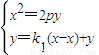 ,消去y得
,消去y得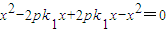 …(1)…(11分)
…(1)…(11分)∵方程(1)有两个根x,x1,∴
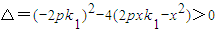
∴
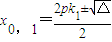 ,x+x1=2pk1,即x1=2pk1-x,同理可得x2=-2pk1-x…(12分)
,x+x1=2pk1,即x1=2pk1-x,同理可得x2=-2pk1-x…(12分)直线MN的斜率
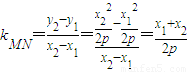 =
=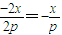 .…(13分)
.…(13分)∴直线MN的斜率等于抛物线C在点A关于对称轴的对称点A1处的切线的斜率.…(14分)
解法二:∵kAM=-kAN…(10分)
∴
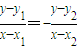 …(11分)
…(11分)将
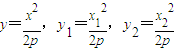 分别代入上式得:
分别代入上式得: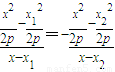 ,
,整理得2x=x1+x2.…(12分)
∴直线MN的
斜率
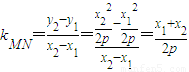 =
=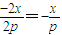 .…(13分)
.…(13分)∴直线MN的斜率等于抛物线C在点A关于对称轴的对称点A1处的切线的斜率.…(14分)
点评:本小题主要考查直线、抛物线、对称等知识,考查数形结合、化归与转化、方程的思想方法,考查数学探究能力以及运算求解能力.

练习册系列答案
相关题目
 设抛物线C:x2=2py(p>0),F为焦点,抛物线C上一点P(m,3)到焦点的距离是4,抛物线C的准线l与y轴的交点为H
设抛物线C:x2=2py(p>0),F为焦点,抛物线C上一点P(m,3)到焦点的距离是4,抛物线C的准线l与y轴的交点为H