题目内容
已知函数f（x）=x3+ax2+bx+c，当x=-1时，取得极大值7，当x=3时，取得极小值，求这个极小值及f（x）的解析式．
解：f′（x）=3x2+2ax+b．
∵当x=-1时，取得极大值7，当x=3时，取得极小值，
∴
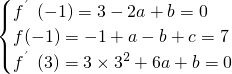，解得
．
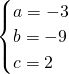∴f′（x）=3x2-6x-9=3（x+1）（x-3），经验证满足题意．
∴f（x）=x3-3x2-9x+2，
∴f（3）=33-3×32-9×3+2=-25．
即当x=3时，取得极小值f（3）=-25．
分析：利用函数f（x）在x=x0取得极值的充要条件f′（x0）=0且f′（x）在x=x0的左右附近符号相反即可得出a，b的值，再利用极大值即可得到c，从而得出答案．
点评：熟练掌握函数f（x）在x=x0取得极值的充要条件是解题的关键．
∵当x=-1时，取得极大值7，当x=3时，取得极小值，
∴
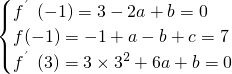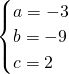，解得．∴f′（x）=3x2-6x-9=3（x+1）（x-3），经验证满足题意．
∴f（x）=x3-3x2-9x+2，
∴f（3）=33-3×32-9×3+2=-25．
即当x=3时，取得极小值f（3）=-25．
分析：利用函数f（x）在x=x0取得极值的充要条件f′（x0）=0且f′（x）在x=x0的左右附近符号相反即可得出a，b的值，再利用极大值即可得到c，从而得出答案．
点评：熟练掌握函数f（x）在x=x0取得极值的充要条件是解题的关键．
练习册系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|