ΧβΡΩΡΎ»ί
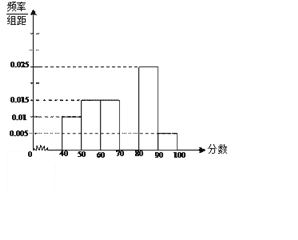
ΓΨΧβΡΩΓΩΡ≥–Θ¥”≤ΈΦ”ΩΦ ‘ΒΡ―ß…ζ÷–≥ι≥ω60Οϊ―ß…ζΘ§ΫΪΤδ≥…Φ®Θ®ΨυΈΣ’ϊ ΐΘ©Ζ÷≥…ΝυΉι[40Θ§50Θ©Θ§[50Θ§60Θ© Θ°Θ°Θ°[90Θ§100]ΚσΘ§Μ≠≥ω»γœ¬≤ΩΖ÷ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ.Ιέ≤λΆΦ–ΈΒΡ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
(Δώ) «σ≥…Φ®¬δ‘Ύ[70Θ§80Θ©…œΒΡΤΒ¬ Θ§≤Δ≤Ι»Ϊ’βΗωΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘΜ
(Δρ) ΙάΦΤ’β¥ΈΩΦ ‘ΒΡΦΑΗώ¬ Θ®60Ζ÷ΦΑ“‘…œΈΣΦΑΗώΘ©ΚΆΤΫΨυΖ÷ΘΜ
(Δσ) …η―ß…ζΦΉΓΔ““ΒΡ≥…Φ® τ”Ύ«χΦδ[40Θ§50Θ©Θ§œ÷¥”≥…Φ® τ”ΎΗΟ«χΦδΒΡ―ß…ζ÷–»Έ―ΓΝΫ»ΥΘ§«σΦΉΓΔ““÷–÷Ν…Ό”–“Μ»Υ±Μ―ΓΒΡΗ≈¬ .
ΓΨ¥πΑΗΓΩΘ®ΔώΘ©ΦϊΫβΈω;(Δρ) 75©΅,71;(Δσ) ![]()
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ
(1) Ήœ»Ω…«σΒΟ≥…Φ®¬δ‘Ύ[70Θ§80Θ©…œΒΡΤΒ¬ «0Θ°3Θ§»ΜΚσ≤Ι»ΪΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΦ¥Ω…ΘΜ
(2)ΫαΚœ(1)ΒΡΫα¬έΩ…ΒΟΦΑΗώ¬ ΈΣ70%Θ§ΤΫΨυΖ÷ΈΣ71ΘΜ
(3)άϊ”ΟΕ‘ΝΔ ¬ΦΰΙΪ ΫΩ…ΒΟΦΉΓΔ““÷–÷Ν…Ό”–“Μ»Υ±Μ―ΓΒΡΗ≈¬ ΈΣ![]() .
.
‘ΧβΫβΈωΘΚ
Θ®ΔώΘ©≥…Φ®¬δ‘Ύ[70Θ§80Θ©…œΒΡΤΒ¬ «0Θ°3Θ§ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γœ¬ΆΦΘ°

(Δρ) ΙάΦΤ’β¥ΈΩΦ ‘ΒΡΦΑΗώ¬ Θ®60Ζ÷ΦΑ“‘…œΈΣΦΑΗώΘ©ΈΣ1-0Θ°01ΓΝ10-0Θ°015ΓΝ10=75©΅
ΤΫΨυΖ÷ΘΚ45ΓΝ0Θ°1+55ΓΝ0Θ°15+65ΓΝ0Θ°15+75ΓΝ0Θ°3+85ΓΝ0Θ°25+95ΓΝ0Θ°05=71
(Δσ) ![]()