题目内容
(2013•湖北)如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A,B,C,D,记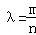 ,△BDM和△ABN的面积分别为S1和S2.
,△BDM和△ABN的面积分别为S1和S2.
(1)当直线l与y轴重合时,若S1=λS2,求λ的值;
(2)当λ变化时,是否存在与坐标轴不重合的直线l,使得S1=λS2?并说明理由.

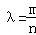 ,△BDM和△ABN的面积分别为S1和S2.
,△BDM和△ABN的面积分别为S1和S2.(1)当直线l与y轴重合时,若S1=λS2,求λ的值;
(2)当λ变化时,是否存在与坐标轴不重合的直线l,使得S1=λS2?并说明理由.

以题意可设椭圆C1和C2的方程分别为
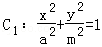 ,
,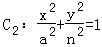 .其中a>m>n>0,
.其中a>m>n>0,
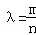 .
.
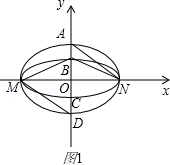
(1)如图1,若直线l与y轴重合,即直线l的方程为x=0,则
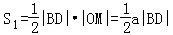 ,
,
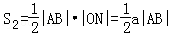 ,
,
所以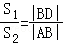 .
.
在C1和C2的方程中分别令x=0,可得yA=m,yB=n,yD=﹣m,
于是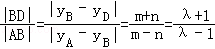 .
.
若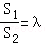 ,则
,则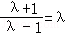 ,化简得λ2﹣2λ﹣1=0,由λ>1,解得
,化简得λ2﹣2λ﹣1=0,由λ>1,解得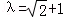 .
.
故当直线l与y轴重合时,若S1=λS2,则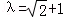 .
.
(2)如图2,若存在与坐标轴不重合的直线l,使得S1=λS2,根据对称性,
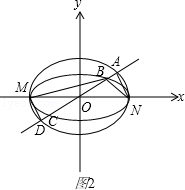
不妨设直线l:y=kx(k>0),
点M(﹣a,0),N(a,0)到直线l的距离分别为d1,d2,则
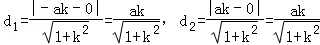 ,所以d1=d2.
,所以d1=d2.
又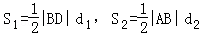 ,所以
,所以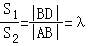 ,即|BD|=λ|AB|.
,即|BD|=λ|AB|.
由对称性可知|AB|=|CD|,所以|BC|=|BD|﹣|AB|=(λ﹣1)|AB|,
|AD|=|BD|+|AB|=(λ+1)|AB|,于是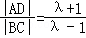 .
.
将l的方程分别与C1和C2的方程联立,可求得
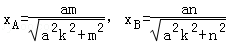
根据对称性可知xC=﹣xB,xD=﹣xA,于是
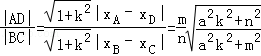 ②
②
从而由①和②可得
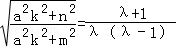 ③
③
令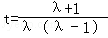 ,则由m>n,可得t≠1,于是由③可得
,则由m>n,可得t≠1,于是由③可得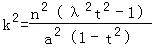 .
.
因为k≠0,所以k2>0.于是③关于k有解,当且仅当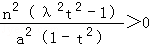 ,
,
等价于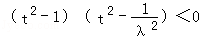 ,由λ>1,解得
,由λ>1,解得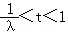 ,
,
即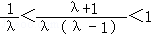 ,由λ>1,解得
,由λ>1,解得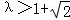 ,所以
,所以
当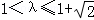 时,不存在与坐标轴不重合的直线l,使得S1=λS2;
时,不存在与坐标轴不重合的直线l,使得S1=λS2;
当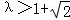 时,存在与坐标轴不重合的直线l,使得S1=λS2.
时,存在与坐标轴不重合的直线l,使得S1=λS2.
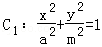 ,
,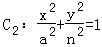 .其中a>m>n>0,
.其中a>m>n>0,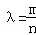 .
.(1)如图1,若直线l与y轴重合,即直线l的方程为x=0,则

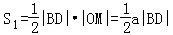 ,
,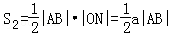 ,
,所以
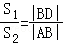 .
.在C1和C2的方程中分别令x=0,可得yA=m,yB=n,yD=﹣m,
于是
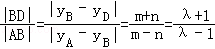 .
.若
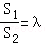 ,则
,则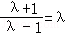 ,化简得λ2﹣2λ﹣1=0,由λ>1,解得
,化简得λ2﹣2λ﹣1=0,由λ>1,解得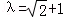 .
.故当直线l与y轴重合时,若S1=λS2,则
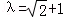 .
.(2)如图2,若存在与坐标轴不重合的直线l,使得S1=λS2,根据对称性,

不妨设直线l:y=kx(k>0),
点M(﹣a,0),N(a,0)到直线l的距离分别为d1,d2,则
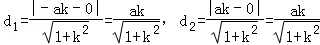 ,所以d1=d2.
,所以d1=d2.又
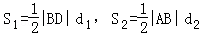 ,所以
,所以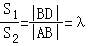 ,即|BD|=λ|AB|.
,即|BD|=λ|AB|.由对称性可知|AB|=|CD|,所以|BC|=|BD|﹣|AB|=(λ﹣1)|AB|,
|AD|=|BD|+|AB|=(λ+1)|AB|,于是
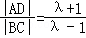 .
.将l的方程分别与C1和C2的方程联立,可求得
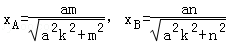
根据对称性可知xC=﹣xB,xD=﹣xA,于是
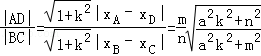 ②
②从而由①和②可得
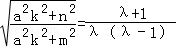 ③
③令
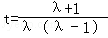 ,则由m>n,可得t≠1,于是由③可得
,则由m>n,可得t≠1,于是由③可得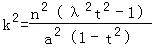 .
.因为k≠0,所以k2>0.于是③关于k有解,当且仅当
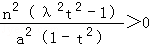 ,
,等价于
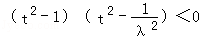 ,由λ>1,解得
,由λ>1,解得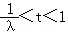 ,
,即
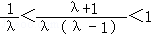 ,由λ>1,解得
,由λ>1,解得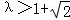 ,所以
,所以当
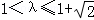 时,不存在与坐标轴不重合的直线l,使得S1=λS2;
时,不存在与坐标轴不重合的直线l,使得S1=λS2;当
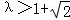 时,存在与坐标轴不重合的直线l,使得S1=λS2.
时,存在与坐标轴不重合的直线l,使得S1=λS2.
练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目
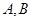 是椭圆
是椭圆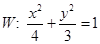 上不关于坐标轴对称的两个点,直线
上不关于坐标轴对称的两个点,直线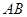 交
交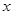 轴于点
轴于点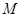 (与点
(与点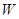 的右焦点,线段
的右焦点,线段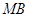 的中点在y轴上,求直线AB的方程;
的中点在y轴上,求直线AB的方程; 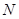 为
为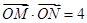 ,直线
,直线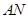 与椭圆
与椭圆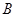 与点
与点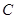 关于
关于 ,
, 距离相等的点的坐标
距离相等的点的坐标 满足的条件.
满足的条件. 的倾斜角的余弦值为________.
的倾斜角的余弦值为________.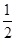 ,m)共线,则实数m=________.
,m)共线,则实数m=________.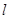 的参数方程为
的参数方程为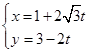 (
(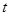 为参数),则直线
为参数),则直线


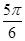
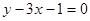 的倾斜角是
的倾斜角是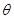 ,则
,则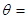 (结果用反三角函数值表示).
(结果用反三角函数值表示).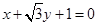 的倾斜角的大小是____________.
的倾斜角的大小是____________.