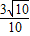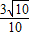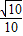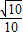题目内容
已知α是第二象限角,且|α+2|≤4,则α的取值范围是
(-
,-π)∪(
,2]
| 3π |
| 2 |
| π |
| 2 |
(-
,-π)∪(
,2]
.| 3π |
| 2 |
| π |
| 2 |
分析:解绝对值不等式|α+2|≤4,可求得-6≤α≤2,再结合已知α是第二象限角,求其交集即可得到α的取值范围.
解答:解:∵|α+2|≤4,
∴-4≤α+2≤4,
∴-6≤α≤2.
又∵α是第二象限角,
∴-
<α<-π或
<α≤2.
故答案为:(-
,-π)∪(
,2].
∴-4≤α+2≤4,
∴-6≤α≤2.
又∵α是第二象限角,
∴-
| 3π |
| 2 |
| π |
| 2 |
故答案为:(-
| 3π |
| 2 |
| π |
| 2 |
点评:本题考查绝对值不等式的解法,考查集合的交、并、补运算,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 是第二象限角,
是第二象限角, ,则
,则 = .
= .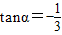 ,则cosα=( )
,则cosα=( )