题目内容
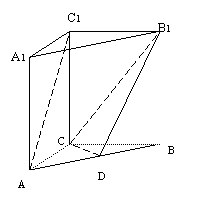
 (理科)如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,CC1>AC,∠ACB=90°,异面直线AC1与BA1所成角的大小为arccos
(理科)如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,CC1>AC,∠ACB=90°,异面直线AC1与BA1所成角的大小为arccos
| ||
| 10 |
(1)求三棱柱ABC-A1B1C1的体积;
(2)设D为线段A1B1的中点,求二面角A-C1D-A1的大小.(结果用反三角函数表示)
分析:(1)欲求三棱柱ABC-A1B1C1的体积,只需求出底面积和高,因为底面为直角三角形,且两条直角边都为2,所以只需求出高CC1,利用异面直线AC1与BA1所成角的大小为arccos
,先借助空间向量,用CC1的长度表示此角的余弦,再与所给的值比较,即可求出CC1,进而求出三棱锥的体积.
(2)利用空间向量来求二面角的大小,只需求出两个半平面的法向量所成角,再结合图形判断法向量所成角是二面角还是其补角.
| ||
| 10 |
(2)利用空间向量来求二面角的大小,只需求出两个半平面的法向量所成角,再结合图形判断法向量所成角是二面角还是其补角.
解答:解:(1)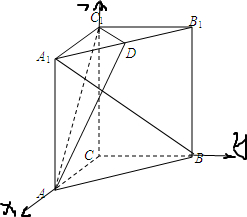 如图,以CA所在直线为ix轴,CB所在直线为y轴,CC1所在直线为z轴建立平面直角坐标系.
如图,以CA所在直线为ix轴,CB所在直线为y轴,CC1所在直线为z轴建立平面直角坐标系.
则A(2,0,0),B(0,2,0),A1(2,O,c),B1(0,2,c),C1(0,0,c)
∴
=(-2,0,c),
=(2,-2,c)
∴cos<
,
>=
=
=
∴c=4,∴CC1=4
S三棱柱ABC-A1B1C1=
AC•BC•CC1=
×2×2×4=8
(2)∵D为线段A1B1的中点,∴D(1,1,4)
∵三棱柱ABC-A1B1C1为直三棱柱,∴AA1⊥平面A1B1C1,
∴
为平面A1B1C1的法向量.
=(0,0,4)
设平面AC1D的法向量为
=(x,y,z)
∵
=(-2,0,4),
=(-1,1,4)
∴-2x+4z=0,-x+y+4z=0
令z=1,则x=2,y=-2,∴
=(2,-2,1)
cos<
,
>=
=
∴平平面A1B1C1的法向量与平面AC1D的法向量所成角为arccos
,
有图知,平平面A1B1C1的法向量与平面AC1D的法向量所成角即为二面角A-C1D-A1,
∴二面角A-C1D-A1的大小为arccos
.
 如图,以CA所在直线为ix轴,CB所在直线为y轴,CC1所在直线为z轴建立平面直角坐标系.
如图,以CA所在直线为ix轴,CB所在直线为y轴,CC1所在直线为z轴建立平面直角坐标系.则A(2,0,0),B(0,2,0),A1(2,O,c),B1(0,2,c),C1(0,0,c)
∴
| AC1 |
| BA1 |
∴cos<
| AC1 |
| BA1 |
| ||||
|
|
| -4+c2 | ||||
|
| ||
| 10 |
∴c=4,∴CC1=4
S三棱柱ABC-A1B1C1=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵D为线段A1B1的中点,∴D(1,1,4)
∵三棱柱ABC-A1B1C1为直三棱柱,∴AA1⊥平面A1B1C1,
∴
| AA1 |
| AA1 |
设平面AC1D的法向量为
| n |
∵
| AC1 |
| AD |
∴-2x+4z=0,-x+y+4z=0
令z=1,则x=2,y=-2,∴
| n |
cos<
| AA1 |
| n |
| 4 | ||
4
|
| 1 |
| 3 |
∴平平面A1B1C1的法向量与平面AC1D的法向量所成角为arccos
| 1 |
| 3 |
有图知,平平面A1B1C1的法向量与平面AC1D的法向量所成角即为二面角A-C1D-A1,
∴二面角A-C1D-A1的大小为arccos
| 1 |
| 3 |
点评:本题主要考查了在直三棱柱中求异面直线所成角,以及二面角的大小的方法,考查了学生的空间想象力,识图能力,以及计算能力.

练习册系列答案
相关题目
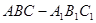 中,
中, ,
,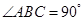 ,
,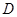 是
是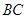 的中点.
的中点.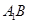 ∥平面
∥平面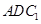 ; (Ⅱ)求二面角
; (Ⅱ)求二面角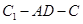 的余弦值;
的余弦值;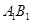 上是否存在点
上是否存在点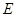 ,使
,使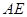 与
与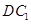 成
成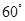 角?若存在,确定
角?若存在,确定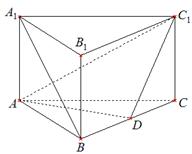
 .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.
 如图, 在直三棱柱
如图, 在直三棱柱 中,
中,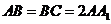 ,
,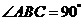 ,
,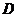 是
是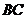 的中点.
的中点.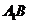 ∥平面
∥平面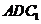 ; (Ⅱ)求二面角
; (Ⅱ)求二面角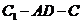 的余弦值;
的余弦值;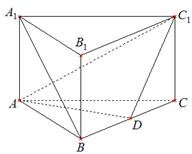 (Ⅲ)(理科)试问线段
(Ⅲ)(理科)试问线段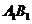 上是否存在点
上是否存在点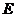 ,使
,使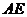 与
与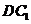 成
成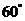 角?若存在,确定
角?若存在,确定