题目内容
20.一个与正四棱锥的底面平行的平面把正四棱锥截成两部分,一部分是棱锥,一部分是棱台,已知被截得的棱台的上、下底面的边长分别是方程x2-6x+8=0的两根,且截得的棱台的侧面积等于此棱台上、下底面面积之和,则该四校锥的高为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{10}{3}$ |
分析 解方程得出棱台的上下底面边长,根据面积关系和比例关系求出棱台的高和小棱锥的高.
解答 解:解方程x2-6x+8=0得x=2或x=4,
∴截得的小棱锥的底面边长是2,截得的棱台的上下底面边长分别为2,4.
设棱台的斜高为h,截得小棱锥的高为h′,
则4×$\frac{1}{2}$(2+4)h=22+42=20,且$\frac{h′}{h′+h}=\frac{2}{4}$
∴h=h′=$\frac{5}{3}$.
∴原来四棱锥的高为h+h′=$\frac{10}{3}$.
故选D.
点评 本题考查了棱锥和棱台的结构特征,画出草图帮助观察各线段的关系比较重要.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
11.设向量$\overrightarrow{a}$=(-3,2),$\overrightarrow{b}$=(cosα,-$\frac{1}{3}$)(0°<α<180°),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则角α为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
15.某人向正东方向走2$\sqrt{3}$千米后,再沿北偏西60°方向走了3千米,结果他离出发点恰好x千米,那么x的值为( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{21-6\sqrt{3}}$ | D. | 3 |
12.若直线l1:ax+2y+6=0与直线l2:x+(a-1)y+(a2-1)=0平行而不重合,则a等于( )
| A. | -1或2 | B. | -1 | C. | 2 | D. | $\frac{2}{3}$ |
10.已知sin(π-α)=-$\frac{2}{5}$,且α是第四象限角,则tanα=( )
| A. | $\frac{2\sqrt{21}}{21}$ | B. | -$\frac{2\sqrt{21}}{21}$ | C. | -$\frac{2}{3}$ | D. | $\frac{\sqrt{21}}{2}$ |
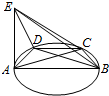 已知三棱锥E-ABD各个面均为直角三角形,且Rt△ADE的直角顶点为A,其中AE=AB,∠ABD=$\frac{π}{6}$,以AB为直径在平面ABD内画圆,且经过点D,任取圆上一点C(不与A,B两点重合).
已知三棱锥E-ABD各个面均为直角三角形,且Rt△ADE的直角顶点为A,其中AE=AB,∠ABD=$\frac{π}{6}$,以AB为直径在平面ABD内画圆,且经过点D,任取圆上一点C(不与A,B两点重合).