题目内容
设x∈R,f(x)=(| 1 | 2 |
(1)请在所给的平面直角坐标系中画出函数f(x)的大致图象;
(2)若不等式f(x)+f(2x)≤k对于任意的x∈R恒成立,求实数k的取值范围.
分析:(1)f(x)=(
)|x|=
,可作出图象;或者先做出x≥0时的函数图象,再根据f(x)是偶函数,图象关于y轴对称,作出x<0的图象.
(2)若不等式f(x)+f(2x)≤k对于任意的x∈R恒成立,只要(f(x)+f(2x))min≤k对于任意的x∈R恒成立即可,
将f(x)的解析式代入,利用换元法转化为二次函数求最值即可.
| 1 |
| 2 |
|
(2)若不等式f(x)+f(2x)≤k对于任意的x∈R恒成立,只要(f(x)+f(2x))min≤k对于任意的x∈R恒成立即可,
将f(x)的解析式代入,利用换元法转化为二次函数求最值即可.
解答: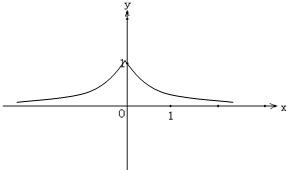 解:(1)如图
解:(1)如图
(2)f(x)=(
)|x|,f(2x)=(
)2|x|
对于任意x∈R,(
)|x|+(
)2|x|≤k恒成立.
令(
)|x|=t∈(0, 1],则y=t2+t(0<t≤1)
对称轴t=-
,则当t=1时,ymax=2,
所以k≥2即可.
 解:(1)如图
解:(1)如图(2)f(x)=(
| 1 |
| 2 |
| 1 |
| 2 |
对于任意x∈R,(
| 1 |
| 2 |
| 1 |
| 2 |
令(
| 1 |
| 2 |
对称轴t=-
| 1 |
| 2 |
所以k≥2即可.
点评:本题考查含有绝对值的函数的图象的做法和不等式恒成立为题,题目难度不大,属基本题型,基本方法的考查.

练习册系列答案
相关题目