题目内容
已知函数f(x)=2x3+(m-x)3(m∈N*).
(1)若x1,x2∈(0,m),证明: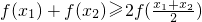 ;
;
(2)对于任意的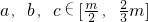 ,问以f(a),f(b),f(c)的值为边长的三条线段是否可构成三角形?并说明理由.
,问以f(a),f(b),f(c)的值为边长的三条线段是否可构成三角形?并说明理由.
(1)证明:由题知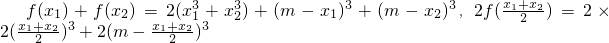 .
.
而 .(2分)
.(2分)
又∵x1,x2∈(0,m),∴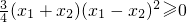 ,
,
∴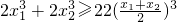 ,(3分)
,(3分)
同理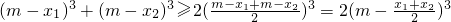 ,(5分)
,(5分)
故得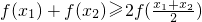 .(6分)
.(6分)
(2)解:以f(a),f(b),f(c)的值为边长的三条线段可以构成三角形.
事实上,因为f(x)=2x3+(m-x)3,所以f'(x)=6x2-3(m-x)2=3x2+6mx-3m2.(7分)
∵当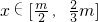 时,f'(x)>0,
时,f'(x)>0,
∴f(x)在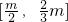 上是增函数,
上是增函数,
∴在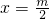 处取得最小值
处取得最小值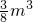 ,在
,在 处取最大值
处取最大值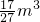 .(9分)
.(9分)
不妨设a≤b≤c,则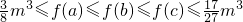 (11分)
(11分)
而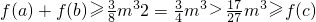 ,
,
因此以f(a),f(b),f(c)的值为边长的三条线段可以构成三角形.(13分)
分析:(1)先分别确定左、右函数值,再利用作差法,即可证得结论;
(2)先证明f(x)在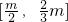 上是增函数,再利用两边之和大于第三边,即可确定结论.
上是增函数,再利用两边之和大于第三边,即可确定结论.
点评:本题考查不等式的证明,考查函数的单调性,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.
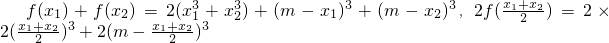 .
.而
 .(2分)
.(2分)又∵x1,x2∈(0,m),∴
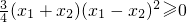 ,
,∴
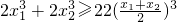 ,(3分)
,(3分)同理
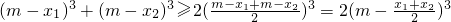 ,(5分)
,(5分)故得
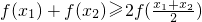 .(6分)
.(6分)(2)解:以f(a),f(b),f(c)的值为边长的三条线段可以构成三角形.
事实上,因为f(x)=2x3+(m-x)3,所以f'(x)=6x2-3(m-x)2=3x2+6mx-3m2.(7分)
∵当
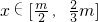 时,f'(x)>0,
时,f'(x)>0,∴f(x)在
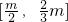 上是增函数,
上是增函数,∴在
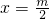 处取得最小值
处取得最小值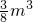 ,在
,在 处取最大值
处取最大值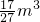 .(9分)
.(9分)不妨设a≤b≤c,则
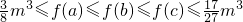 (11分)
(11分)而
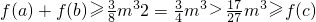 ,
,因此以f(a),f(b),f(c)的值为边长的三条线段可以构成三角形.(13分)
分析:(1)先分别确定左、右函数值,再利用作差法,即可证得结论;
(2)先证明f(x)在
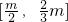 上是增函数,再利用两边之和大于第三边,即可确定结论.
上是增函数,再利用两边之和大于第三边,即可确定结论.点评:本题考查不等式的证明,考查函数的单调性,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目