��Ŀ����
����С������12�֣�����f(x)=ax2��2(a��1)x��2lnx ,a>0
(1)����f(x)�ĵ������䣻
(2)���ں���ͼ���ϵIJ�ͬ����A(x1,y1),B(x2,y2)������ں���ͼ���ϴ��ڵ�P(x0,y0)������x0��x1��x2֮�䣩��ʹ�õ�P��������lƽ����ֱ��AB�����AB���ڡ��������ߡ�����x0= 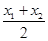 ʱ���ֳ�AB���ڡ���ֵ�������ߡ�.���ʣ��ں���f(x)��ͼ�����Ƿ���ڲ�ͬ����A,B��ʹ��AB���ڡ���ֵ�������ߡ��������ڣ����A,B�����ꣻ�������ڣ�˵������
ʱ���ֳ�AB���ڡ���ֵ�������ߡ�.���ʣ��ں���f(x)��ͼ�����Ƿ���ڲ�ͬ����A,B��ʹ��AB���ڡ���ֵ�������ߡ��������ڣ����A,B�����ꣻ�������ڣ�˵������
(1) ����������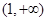 ���ݼ�������
���ݼ������� (2)
(2)
����������1������������ĵ�����Ȼ����ݵ���֪ʶ��������ĵ������䣻��2�������Ƿ�������⣬�ȼ�����ڣ��ѽ��۵����������캯�������õ������ó������ĵ����ԣ������õ����Եó�����ʽ���Ƴ�����֪����ì�ܣ��ó����費����
�⣺��1��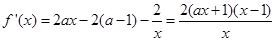 ��
��
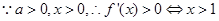 ��
��
���ԣ�����������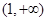 ���ݼ�������
���ݼ������� ��������������������������������6��
��������������������������������6��
��2��������ڲ�ͬ���� ����������
����������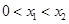 ����ʹ��
����ʹ�� ���ڡ���ֵ�������ߡ�����
���ڡ���ֵ�������ߡ�����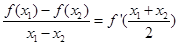 ��������������������������������7��
��������������������������������7��
����ã�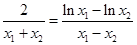 ����
����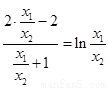 ������������������������8��
������������������������8��
�躯��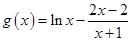 ����
����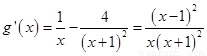 ��
��
�� ʱ��
ʱ��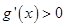 ����
����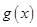 ��
��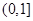 ������������������������������10��
������������������������������10��
��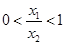 ������
������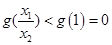 ����
����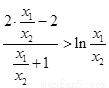 �����������ì�ܣ�
�����������ì�ܣ�
�����ں���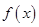 ��ͼ�����Dz����ڲ�ͬ����
��ͼ�����Dz����ڲ�ͬ����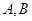 ��ʹ��
��ʹ�� ���ڡ���ֵ�������ߡ�.12��
���ڡ���ֵ�������ߡ�.12��
