题目内容
过点M(3,-4)且在两坐标轴上的截距相等的直线的方程为( )A.x+y+1=0
B.4x+3y=0
C.x+y+2=0
D.x+y+1=0或 4x+3y=0
【答案】分析:当直线过原点时,求出斜率,斜截式写出直线方程,并化为一般式.当直线不过原点时,设直线的方程为 x+y+m=0,把P(3,-4)代入直线的方程,求出m值,可得直线方程.
解答:解:当直线过原点时,斜率等于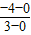 =-
=- ,故直线的方程为y=-
,故直线的方程为y=- x,即4x+3y=0
x,即4x+3y=0
当直线不过原点时,设直线的方程为 x+y+m=0,把P(3,-4)代入直线的方程得 m=1,
故求得的直线方程为 x+y+1=0,
综上,满足条件的直线方程为4x+3y=0或x+y+1=0
故选:D.
点评:本题考查求直线方程的方法,待定系数法求直线的方程是一种常用的方法,体现了分类讨论的数学思想.
解答:解:当直线过原点时,斜率等于
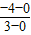 =-
=- ,故直线的方程为y=-
,故直线的方程为y=- x,即4x+3y=0
x,即4x+3y=0当直线不过原点时,设直线的方程为 x+y+m=0,把P(3,-4)代入直线的方程得 m=1,
故求得的直线方程为 x+y+1=0,
综上,满足条件的直线方程为4x+3y=0或x+y+1=0
故选:D.
点评:本题考查求直线方程的方法,待定系数法求直线的方程是一种常用的方法,体现了分类讨论的数学思想.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目