题目内容
设
，函数
有意义, 实数
取值范围 .
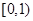
解析试题分析：由题意得，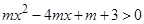
对都成立，当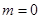
时，显然成立，或当
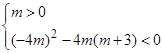即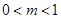
时不等式也成立，所以实数取值范围.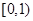
考点：对数函数的定义域、一元二次不等式.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
天天向上一本好卷系列答案小学生10分钟应用题系列答案题目内容
设，函数有意义, 实数取值范围 .
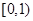
解析试题分析：由题意得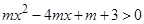，对都成立，当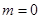时，显然成立，或当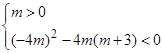即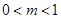时不等式也成立，所以实数取值范围.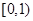
考点：对数函数的定义域、一元二次不等式.
天天向上一本好卷系列答案小学生10分钟应用题系列答案
的判断：
与
的图象关于直线
对称；
为偶函数，且
，则
，且
，
，
，若
，则
，
，使得
.
与
的图象的交点为
，且
，则
= .
时，则下列结论正确的是 .
，等式
恒成立
，使得方程
有两个不等实数根
，若
，则一定有
，使得函数
在
上有三个零点
的定义域为 .
，使
成立，则实数
的取值范围是 .
是定义在
上的偶函数，当
时，
.若
，则实数
的值为 .
是函数
的切线，则实数
．
的单调递减区间为_______