题目内容
直线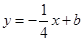
是函数
的切线，则实数
．
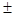1
解析试题分析：先对函数求导，即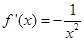
，由于切线方程为
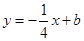，所以，
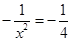，解得：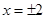
，因此，切点为（2，
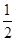）或（－2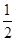，－），代入切线方程，可得
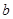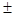＝1.
考点：函数的导数求法，函数导数的几何意义.
练习册系列答案
名校课堂系列答案
相关题目
题目内容
直线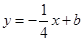是函数的切线，则实数 ．
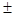1
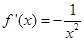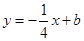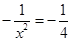解析试题分析：先对函数求导，即，由于切线方程为，所以，，解得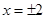：，因此，切点为（2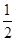，）或（－2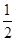，－），代入切线方程，可得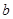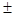＝1.
考点：函数的导数求法，函数导数的几何意义.
名校课堂系列答案
是周期为5的奇函数，且满足
，则
= .
，函数
有意义, 实数
取值范围 .
的定义域为 .
与
的图像关于直线
对称，则
.
的定义域是 ．
的图象与
的图象关于直线
对称，则函数
）处的切线方程为 ．
是奇函数，则a= 。
，
有下面四个结论：
是奇函数； （2）
恒成立；
的最大值是
； (4) 
.