题目内容
 如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2.
如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2.(Ⅰ)若P为抛物线的焦点,求a的值,并确定抛物线的准线与以AB为直径的圆的位置关系.
(Ⅱ)试证明:k1+k2为定值.
分析:(I)由直线方程算出P(4,0),从而得出a=8.设A(x1,y1)、B(x2,y2),根据抛物线的定义列式,化简可得M到准线的距离d恰好等于圆的半径,从而得到直线与圆相切.
(II)直线l与抛物线消去x,得y2-2amy-8a=0,利用根与系数的关系将k1+k2化成关于A、B坐标的式子,化简整理可得k1+k2=0,即k1+k2为定值.
(II)直线l与抛物线消去x,得y2-2amy-8a=0,利用根与系数的关系将k1+k2化成关于A、B坐标的式子,化简整理可得k1+k2=0,即k1+k2为定值.
解答:解:(Ⅰ)由直线l:x=my+4得点P(4,0),故
=4⇒a=8…(2分)
设交点A(x1,y1),B(x2,y2),它们的中点M(
,
),
设点M到抛物线的准线的距离为d,则d=
+4,…(4分)
∵r=
|AB|=
=
+4=d,
∴抛物线的准线与以AB为直径的圆相切.…(6分)
(Ⅱ)由直线l:x=my+4得点P(4,0),∴Q(-4,0),
将直线l:x=my+4与抛物线的方程y2=2ax联立得y2-2amy-8a=0,
∵△>0恒成立,
…(9分)
∴k1+k2=
+
=
=
…(11分)
即k1+k2=
,代入(*)得k1+k2=0,故k1+k2为定值得征.…(13分)
| a |
| 2 |
设交点A(x1,y1),B(x2,y2),它们的中点M(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
设点M到抛物线的准线的距离为d,则d=
| x1+x2 |
| 2 |
∵r=
| 1 |
| 2 |
| x1+4+x2+4 |
| 2 |
| x1+x2 |
| 2 |
∴抛物线的准线与以AB为直径的圆相切.…(6分)
(Ⅱ)由直线l:x=my+4得点P(4,0),∴Q(-4,0),
将直线l:x=my+4与抛物线的方程y2=2ax联立得y2-2amy-8a=0,
∵△>0恒成立,
|
|
∴k1+k2=
| y1 |
| x1+4 |
| y2 |
| x2+4 |
=
| y1(x2+4)+y2(x1+4) |
| (x1+4)(x2+4) |
| y1(my2+8)+y2(my1+8) |
| (x1+4)(x2+4) |
即k1+k2=
| 2my1y2+8(y1+y2) |
| (x1+4)(x2+4) |
点评:本题给出抛物线的焦点弦为直径的圆,求该圆与准线的位置关系.着重考查了抛物线的定义、简单几何性质,直线与圆的位置关系和直线的斜率等知识,属于中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 如图,已知直线l:x=my+1过椭圆
如图,已知直线l:x=my+1过椭圆 如图,已知直线L:x=my+1过椭圆C:
如图,已知直线L:x=my+1过椭圆C: (2012•乐山二模)如图,已知直线L:x=my+1过椭圆C:
(2012•乐山二模)如图,已知直线L:x=my+1过椭圆C: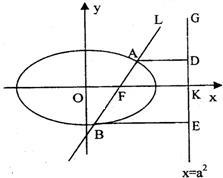 如图,已知直线L:
如图,已知直线L: