题目内容
已知函数 是定义在R上的偶函数,且对任意
是定义在R上的偶函数,且对任意 ,都有
,都有 。当
。当 时,
时, 设函数
设函数 上的反函数为
上的反函数为 则
则 的值为( )
的值为( )
A. | B. | C. | D. |
D
解析试题分析:设f-1(19)=a∈[-2,0],则f(a)=19,
∵a∈[-2,0],∴-a∈[0,2],∴(-a+4)∈[4,6],
又已知f(x)是定义在R上的偶函数,∴f(a)=f(-a),
∵对任意x∈R,都有f(x)=f(x+4),∴f(-a)=f(-a+4),
而当x∈[4,6]时,f(x)=2x+1,
∴f(-a+4)=2-a+4+1
∴2-a+4+1=19,即2-a+4=18,即-a+4=log218,
而log218=1+2log23,∴-a+4=1+2log23,∴a=3-2log23.
故选D.
考点:本题主要考查了函数的奇偶性、周期性及反函数.
点评:准确理解以上有关定义及性质是解决问题的关键, 利用函数的奇偶性、周期性及反函数,把要求的函数的自变量转化到所给的区间x∈[4,6],即可计算出要求的值

练习册系列答案
相关题目
若函数 与
与 的图象有交点,则
的图象有交点,则 的取值范围是( )
的取值范围是( )
A. 或 或  | B. |
C. | D. |
若二次函数 的部分图像如右图所示,则函数
的部分图像如右图所示,则函数 的零点所在的区间是( )
的零点所在的区间是( )
A. | B.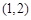 | C. | D. |
已知 ,那么
,那么 用
用 表示是( )
表示是( )
A.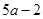 | B. | C. | D. |
已知函数 ,则
,则 ( )
( )
| A.4 | B. | C.-4 | D.- |
若指数函数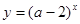 在
在 上是减函数,那么( )
上是减函数,那么( )
A. | B. | C. | D. |
若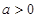 ,且
,且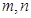 为整数,则下列各式中正确的是
为整数,则下列各式中正确的是
A. | B. |
C. | D. |
函数f (x)=(m2-m-1)x 是幂函数,且在x∈(0,+∞)上是减函数,那么实数
是幂函数,且在x∈(0,+∞)上是减函数,那么实数
m的值为
A. | B.-2 | C. | D.2 |
已知函数 ,则
,则 =( )
=( )
A. | B. | C. | D. |