题目内容
若二次函数 的部分图像如右图所示,则函数
的部分图像如右图所示,则函数 的零点所在的区间是( )
的零点所在的区间是( )
A. | B.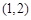 | C. | D. |
C
解析试题分析:因为 的部分图像如右图所示,所以
的部分图像如右图所示,所以 。
。 =
= ,g(
,g( )=ln
)=ln +1-b<0,g(1)=ln1+2-b=2-b>0,
+1-b<0,g(1)=ln1+2-b=2-b>0,
所以函数g(x)=lnx+f′(x)的零点所在的区间是 。
。
考点:二次函数的性质;函数的零点;导数的运算。
点评:零点存在性定理只能判定零点的存在性,不能判断零点的个数。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知幂函数 的图象过点
的图象过点 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知函数 ,且
,且 ,则实数
,则实数 的值为( )
的值为( )
A. | B. | C. 或 或 | D. 或 或 或 或 |
已知定义在 上的函数
上的函数 满足
满足 ,且
,且
 ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于 ,则
,则 等于( )
等于( )
| A.4 | B.6 | C.5 | D.7 |
已知定义在 上的函数
上的函数 满足
满足 ,且
,且 ,
,  ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于 ,则
,则 等于( )
等于( )
| A.4 | B.5 | C.6 | D.7 |
2log510+log50.25=
| A.0 | B.1 | C.2 | D.4 |
已知函数 是定义在R上的偶函数,且对任意
是定义在R上的偶函数,且对任意 ,都有
,都有 。当
。当 时,
时, 设函数
设函数 上的反函数为
上的反函数为 则
则 的值为( )
的值为( )
A. | B. | C. | D. |
已知幂函数 过点
过点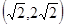 ,则函数
,则函数 的表达式为( )
的表达式为( )
A. | B. | C. | D.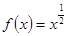 |
 ,函数
,函数 与
与 的图像可能是( )
的图像可能是( )