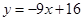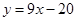题目内容
已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( )
| A.-1<a<2 | B.-3<a<6 | C.a<-1或a>2 | D.a<-3或a>6 |
D
试题分析:因为f(x)=x3+ax2+(a+6)x+1有极大值和极小值,所以方程
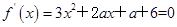 由不等实根,即
由不等实根,即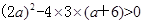 ,解得a<-3或a>6
,解得a<-3或a>6,故选D。
点评:典型题,利用导数求函数的极值,是高考常见题目。求极值的步骤:计算导数、求驻点、讨论驻点附近导数的正负、确定极值。

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
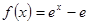
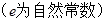 ,则该函数曲线在
,则该函数曲线在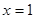 处的切线方程是( )
处的切线方程是( ) 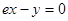
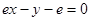
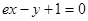
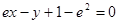
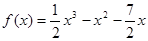 ,则
,则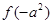 与
与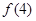 的大小关系为( )
的大小关系为( )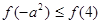 B.
B.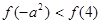
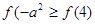 D
D 在曲线
在曲线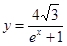 上,
上, 为曲线在点
为曲线在点
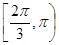
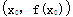 为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题:
为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题: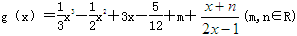 ,
,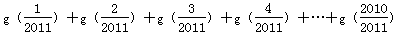 = .
= . ,
,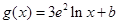 (
(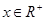 ,
,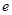 为常数,
为常数,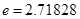 ),且这两函数的图像有公共点,并在该公共点处的切线相同.
),且这两函数的图像有公共点,并在该公共点处的切线相同.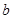 的值;
的值;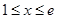 时,
时, 恒成立,求实数
恒成立,求实数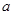 的取值范围.
的取值范围.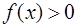 ,则当
,则当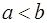 时,定积分
时,定积分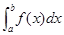 的符号( )
的符号( )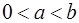 时是正的,当
时是正的,当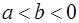 时是负的
时是负的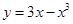 上切点为
上切点为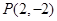 的切线方程是( )
的切线方程是( )