题目内容
(本题满分18分,第(1)小题4分,第2小题6分,第3小题8分)
已知函数![]() ,实数
,实数![]() 且
且![]() 。
。
(1)设![]() ,判断函数
,判断函数![]() 在
在![]() 上的单调性,并说明理由;
上的单调性,并说明理由;
(2)设![]() 且
且![]() f(x)的定义域和值域都是
f(x)的定义域和值域都是![]() ,求
,求![]() 的最大值;
的最大值;
(3) 若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的范围;
的范围;
(本题满分18分,第(1)小题4分,第2小题6分,第3小题8分)
解:(1)设![]() ,则
,则![]() ,
,
…………………………………………………. 2分
![]()
![]() ,
,![]() ,
,![]() ,
,
即![]() ,因此函数
,因此函数![]() 在
在![]() 上的单调递增。
上的单调递增。
…………………………………………………. 4分
(2)由(1)及![]() 的定义域和值域都是
的定义域和值域都是![]() 得
得![]() ,
,
因此![]() 是方程
是方程![]() 的两个不相等的正数根,
的两个不相等的正数根,
…………………………………………………. 6分
等价于方程![]() 有两个不等的正数根,
有两个不等的正数根,
即![]() ,
,
解得![]() ,
,
…………………………………………………. 8分
![]() ,
,
![]() ,
,![]()
![]() 时,
时,![]() 最大值为
最大值为![]() 。
。
…………………………………………………. 10分
(3)![]() ,则不等式
,则不等式![]() 对
对![]() 恒成立,即
恒成立,即![]() 即不等式
即不等式 ,对
,对![]() 恒成立,
恒成立,
…………………………………………………. 12分
令h(x)=![]() ,易证h(x)在
,易证h(x)在![]() 递增,同理
递增,同理![]()
![]() 递减。
递减。
…………………………………………………. 14分
![]() ,
,
…………………………………………………. 16分
![]()
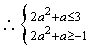
![]() 。
。
…………………………………………………. 18分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时
时 的周期数列,当
的周期数列,当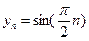 时
时 是周期为
是周期为 的周期数列。
的周期数列。 满足
满足 (
( (
( 不同时为0),且数列
不同时为0),且数列 的周期数列,求常数
的周期数列,求常数 的值;
的值; ,且
,且 .
. ,试判断数列
,试判断数列 ,试判断数列
,试判断数列 (
( ,
,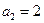 ,
, ,数列
,数列 的前
的前 ,使对任意的
,使对任意的 成立,若存在,求出
成立,若存在,求出 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时
时 的周期数列,当
的周期数列,当 时
时 是周期为
是周期为 的周期数列。
的周期数列。 满足
满足 (
( (
(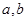 不同时为0),且数列
不同时为0),且数列 的周期数列,求常数
的周期数列,求常数 的值;
的值; ,且
,且 .
.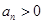 ,试判断数列
,试判断数列 ,试判断数列
,试判断数列 (
(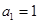 ,
,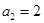 ,
, ,数列
,数列 的前
的前 ,使对任意的
,使对任意的 成立,若存在,求出
成立,若存在,求出 ,其中
,其中 .
. 时,设
时,设 ,
, ,求
,求 的解析式及定义域;
的解析式及定义域; 时,求
时,求 的最小值;
的最小值; ,当
,当 时,
时, 对任意
对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围. 是等差数列,且公差为
是等差数列,且公差为 ,若数列
,若数列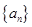 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”. ,求证:该数列是“封闭数列”;
,求证:该数列是“封闭数列”; 是否是“封闭数列”,为什么?
是否是“封闭数列”,为什么? 是数列
是数列 项和,若公差
项和,若公差 ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使 ;若存在,求
;若存在,求