题目内容
甲、乙两人参加一次交通知识考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.(Ⅰ)求甲、乙两人考试均合格的概率;
(Ⅱ)求甲答对试题数ξ的概率分布及数学期望.
分析:(I)甲、乙两人考试均合格表示两个人同时合格,两个人都合格是相互独立的,做出两个人分别合格的概率,利用相互独立事件同时发生的概率得到结果.
(II)甲答对试题数ξ依题意知ξ=0,1,2,3,结合变量对应的事件和等可能事件的概率公式,得到变量的概率,写出分布列.做出期望值.
(II)甲答对试题数ξ依题意知ξ=0,1,2,3,结合变量对应的事件和等可能事件的概率公式,得到变量的概率,写出分布列.做出期望值.
解答:解:(Ⅰ)设甲、乙两人参加交通知识考试合格的事件分别为A、B
P(A)=
=
=
,
P(B)=
=
=
.
∵事件A、B相互独立,
∴甲、乙两人考试均合格的概率为P(A•B)=
×
=
.
即甲、乙两人考试均合格的概率为
.
(Ⅱ)甲答对试题数ξ依题意知ξ=0,1,2,3,
p(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
P(ξ=3)=
=
.
∴ξ的分布列如下:
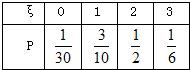
∴甲答对试题数ξ的数学期望Eξ=0×
+1×
+2×
+3×
=
.
P(A)=
| ||||||
|
| 60+20 |
| 120 |
| 2 |
| 3 |
P(B)=
| ||||||
|
| 56+56 |
| 120 |
| 14 |
| 15 |
∵事件A、B相互独立,
∴甲、乙两人考试均合格的概率为P(A•B)=
| 2 |
| 3 |
| 14 |
| 15 |
| 28 |
| 45 |
即甲、乙两人考试均合格的概率为
| 28 |
| 45 |
(Ⅱ)甲答对试题数ξ依题意知ξ=0,1,2,3,
p(ξ=0)=
| ||
|
| 1 |
| 30 |
P(ξ=1)=
| ||||
|
| 3 |
| 10 |
P(ξ=2)=
| ||||
|
| 1 |
| 2 |
P(ξ=3)=
| ||
|
| 1 |
| 6 |
∴ξ的分布列如下:

∴甲答对试题数ξ的数学期望Eξ=0×
| 1 |
| 30 |
| 3 |
| 10 |
| 1 |
| 2 |
| 1 |
| 6 |
| 9 |
| 5 |
点评:本题考查离散型随机变量的分布列和期望,考查等可能事件的概率,考查利用概率知识解决实际问题的能力,是一个比较好的概率解答题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目