题目内容
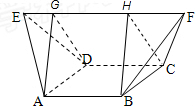
如图所示,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE,△BCF均为正三角形,EF∥AB,EF=2,则该多面体的体积为______.


过AD做底面ABCD垂直的平面交EF于G点
过BC做底面ABCD垂直的平面交EF于H点
则多面体ABCDEF被分为三棱锥E-ADG,三棱柱ADG-BCH,三棱锥F-HBC三个部分
由ABCD是边长为1的正方形,且△ADE,△BCF均为正三角形,EF∥AB,EF=2,
易得EG=HF=
,GH=1
S△ADG=S△BCH=
∴VE-ADG=VF-HBC=
,VADG-BCH=
∴多面体ABCDEF的体积V=2×
+
=
故答案为:
过BC做底面ABCD垂直的平面交EF于H点
则多面体ABCDEF被分为三棱锥E-ADG,三棱柱ADG-BCH,三棱锥F-HBC三个部分
由ABCD是边长为1的正方形,且△ADE,△BCF均为正三角形,EF∥AB,EF=2,
易得EG=HF=
| 1 |
| 2 |
S△ADG=S△BCH=
| ||
| 4 |
∴VE-ADG=VF-HBC=
| ||
| 24 |
| ||
| 4 |
∴多面体ABCDEF的体积V=2×
| ||
| 24 |
| ||
| 4 |
| ||
| 3 |
故答案为:
| ||
| 3 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目