题目内容
在△ABC中,AB边上的中线CO=4,若动点P满足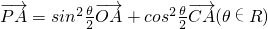 ,则
,则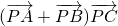 的最小值是________.
的最小值是________.
-8
分析:令λ= ,0≤λ≤1,可得
,0≤λ≤1,可得  =
= +(λ-1)
+(λ-1) ,再由
,再由  =
= -
- 可得-
可得- =(λ-1)
=(λ-1) .故要求的式子可化为 2λ(λ-1)•16,再利用二次函数的性质求得它的最小值.
.故要求的式子可化为 2λ(λ-1)•16,再利用二次函数的性质求得它的最小值.
解答:令λ= ,0≤λ≤1,则1-λ=
,0≤λ≤1,则1-λ=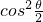 ,
,
∴ =λ
=λ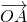 +(1-λ)
+(1-λ) =
= +(λ-1)
+(λ-1) .
.
再由 =
= -
- 可得-
可得- =(λ-1)
=(λ-1) .
.
故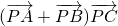 =
=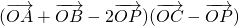 =
=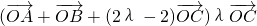
=2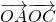 +2
+2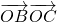 +2(λ-1)λ
+2(λ-1)λ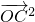 =2λ(λ-1)•16,
=2λ(λ-1)•16,
故当λ= 时,2λ(λ-1)8 取得最小值为-8,
时,2λ(λ-1)8 取得最小值为-8,
故答案为-8.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的运算,二次函数的性质应用,属于中档题.
分析:令λ=
 ,0≤λ≤1,可得
,0≤λ≤1,可得  =
= +(λ-1)
+(λ-1) ,再由
,再由  =
= -
- 可得-
可得- =(λ-1)
=(λ-1) .故要求的式子可化为 2λ(λ-1)•16,再利用二次函数的性质求得它的最小值.
.故要求的式子可化为 2λ(λ-1)•16,再利用二次函数的性质求得它的最小值.解答:令λ=
 ,0≤λ≤1,则1-λ=
,0≤λ≤1,则1-λ=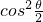 ,
,∴
 =λ
=λ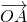 +(1-λ)
+(1-λ) =
= +(λ-1)
+(λ-1) .
.再由
 =
= -
- 可得-
可得- =(λ-1)
=(λ-1) .
.故
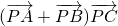 =
=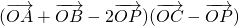 =
=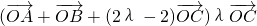
=2
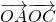 +2
+2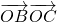 +2(λ-1)λ
+2(λ-1)λ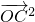 =2λ(λ-1)•16,
=2λ(λ-1)•16,故当λ=
 时,2λ(λ-1)8 取得最小值为-8,
时,2λ(λ-1)8 取得最小值为-8,故答案为-8.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的运算,二次函数的性质应用,属于中档题.

练习册系列答案
相关题目
 如图,在△ABC中,AB=BC=4,∠ABC=30°,AD是边BC′上的高,则
如图,在△ABC中,AB=BC=4,∠ABC=30°,AD是边BC′上的高,则| AD |
| AC |
| A、0 | B、4 | C、8 | D、-4 |
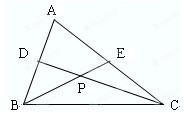 如图,在△ABC中,
如图,在△ABC中,