题目内容
如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点.(1)求异面直线A1D与BC所成角的大小(结果用反三角函数值表示);
(2)求直线A1B1到平面DAB的距离.
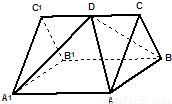
【答案】分析:(1)可通过建立空间直角坐标系,利用向量坐标运算求向量的夹角来求异面直线所成的角;或通过作平行线,再解三角形求解;
(2)根据转化思想,线面距离转化为点到平面的距离,再利用三棱锥的换底性求解.
解答: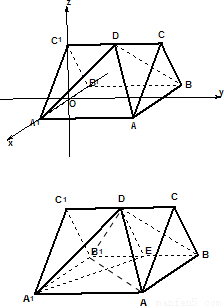 解:(1)方法一:
解:(1)方法一:
以A1B1中点O为坐标原点,如图建立空间直角坐标系.
由题意得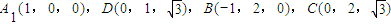
则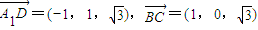
设θ为向量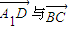 的夹角,
的夹角,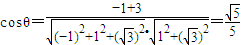 ,
,
∴异面直线A1D与BC所成角的大小为arccos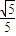 .
.
方法二:取B1B中点E,连结A1E,DE.∵DE∥CB
∴∠A1DE为异面直线A1D与BC所成的角.
在Rt△A1B1E中,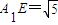 ;在Rt△A1C1D中,
;在Rt△A1C1D中,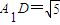 ;
;
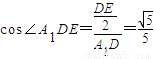 .
.
∴异面直线A1D与BC所成角的大小为arccos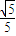 .
.
(2)∵AB∥A1B1,∴A1B1∥平面ABD,
∴A1B1到平面DAB的距离即为A1到平面DAB的距离,设为h.
由题意得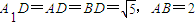 ,
,
等腰△ADB底边AB上的高为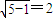 ,
,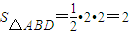 ,则
,则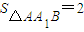 ,
,
且D到平面ABB1A1的距离为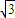 ,
,
由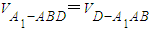 得
得
 ×S△ABD•h=
×S△ABD•h= ×
×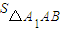 ×
×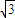 ,
,
∴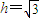 ,
,
∴直线A1B1到平面DAB的距离为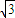 .
.
点评:本题考查异面直线所成的角及线面距离问题.
(2)根据转化思想,线面距离转化为点到平面的距离,再利用三棱锥的换底性求解.
解答:
 解:(1)方法一:
解:(1)方法一:以A1B1中点O为坐标原点,如图建立空间直角坐标系.
由题意得
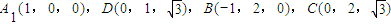
则
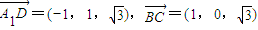
设θ为向量
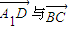 的夹角,
的夹角,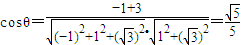 ,
,∴异面直线A1D与BC所成角的大小为arccos
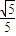 .
.方法二:取B1B中点E,连结A1E,DE.∵DE∥CB
∴∠A1DE为异面直线A1D与BC所成的角.
在Rt△A1B1E中,
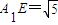 ;在Rt△A1C1D中,
;在Rt△A1C1D中,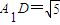 ;
;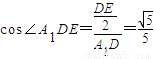 .
.∴异面直线A1D与BC所成角的大小为arccos
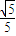 .
.(2)∵AB∥A1B1,∴A1B1∥平面ABD,
∴A1B1到平面DAB的距离即为A1到平面DAB的距离,设为h.
由题意得
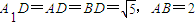 ,
,等腰△ADB底边AB上的高为
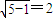 ,
,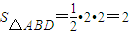 ,则
,则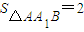 ,
,且D到平面ABB1A1的距离为
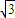 ,
,由
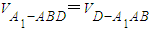 得
得 ×S△ABD•h=
×S△ABD•h= ×
×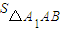 ×
×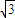 ,
,∴
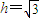 ,
,∴直线A1B1到平面DAB的距离为
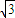 .
.点评:本题考查异面直线所成的角及线面距离问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知△ABC的顶点为A(2,4),B(0,-2),C(-2,3),求:
如图,已知△ABC的顶点为A(2,4),B(0,-2),C(-2,3),求: 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证: 如图,已知两点A(-
如图,已知两点A(-
 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,