题目内容
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API | 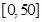 | 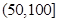 | 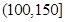 | 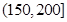 | 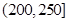 | 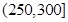 | 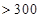 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
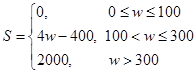 ,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染完成下面
 列联表,并判断能否有
列联表,并判断能否有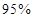 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?附:
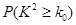 | 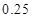 | 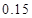 | 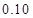 | 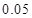 | 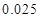 | 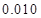 | 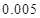 | 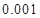 |
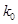 | 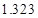 | 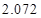 | 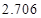 | 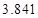 | 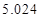 | 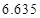 | 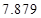 | 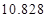 |
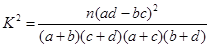
| | 非重度污染 | 重度污染 | 合计 |
| 供暖季 | | | |
| 非供暖季 | | | |
| 合计 | | | 100 |
(1)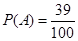 ;(2)有95%的把握认为空气重度污染与供暖有关
;(2)有95%的把握认为空气重度污染与供暖有关
解析试题分析:(1)根据所给数据,求出经济损失S大于200元且不超过600元的天数的频率,以此频率作为“在本年内随机抽取一天,该天经济损失S大于200元且不超过600元”的概率(估计)
(2)由于总共有15天为重度污染,其中有8天在供暖季,那么有7天在非供暖季;在30天供暖季中有8天为重度污染,那么有22天为非重度污染;非重度污染有85天其中有22天在供暖季,那么有63天在非供暖季,由此可完成 列联表:
列联表:
代入公式 非重度污染 重度污染 合计 供暖季 22 8 30 非供暖季 63 7 70 合计 85 15 100 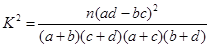 即可求得K2的观测值,从而确定是否有95%的把握认为空气重度污染与供暖有关
即可求得K2的观测值,从而确定是否有95%的把握认为空气重度污染与供暖有关
试题解析:(1)设“在本年内随机抽取一天,该天经济损失S大于200元且不超过600元”为事件A
1分
由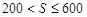 ,得
,得 ,频数为39, 3分
,频数为39, 3分
所以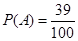 4分
4分
(2)根据以上数据得到如下列联表:
8分 非重度污染 重度污染 合计 供暖季 22 8 30 非供暖季 63 7 70 合计 85 15 100
K2的观测值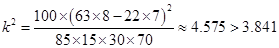 10分
10分
所以有95%的把握认为空气重度污染与供暖有关 12分
考点:1、概率与统计;2、函数的应用

某医院一天派出医生下乡医疗,派出医生人数及其概率如下:
| 医生人数 | 0 | 1 | 2 | 3 | 4 | 5人及以上 |
| 概率 | 0.1 | 0.16 | x | y | 0.2 | z |
(2)若派出医生最多4人的概率为0.96,最少3人的概率为0.44,求y、z的值.
某公司销售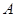 、
、 、
、 三款手机,每款手机都有经济型和豪华型两种型号,据统计
三款手机,每款手机都有经济型和豪华型两种型号,据统计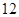 月份共销售
月份共销售 部手机(具体销售情况见下表)
部手机(具体销售情况见下表)
| | 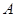 款手机 款手机 |  款手机 款手机 |  款手机 款手机 |
| 经济型 | 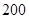 | 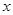 | 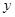 |
| 豪华型 | 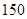 | 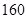 | 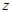 |
 部手机中,经济型
部手机中,经济型 款手机销售的频率是
款手机销售的频率是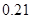 .
.(1)现用分层抽样的方法在
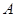 、
、 、
、 三款手机中抽取
三款手机中抽取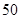 部,求在
部,求在 款手机中抽取多少部?
款手机中抽取多少部?(2)若
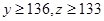 ,求
,求 款手机中经济型比豪华型多的概率.
款手机中经济型比豪华型多的概率. 公安部交管局修改后的酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其判断标准是驾驶人员每100毫升血液中的酒精含量X毫克,当20≤X<80时,认定为酒后驾车;当X≥80时,认定为醉酒驾车,重庆市公安局交通管理部门在对G42高速路我市路段的一次随机拦查行动中,依法检测了200辆机动车驾驶员的每100毫升血液中的酒精含量,酒精含量X(单位:毫克)的统计结果如下表:
| X | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,+∞) |
| 人数 | t | 1 | 1 | 1 | 1 | 1 |
(1)求t的值;
(2)从酒后违法驾车的司机中随机抽取2人,求这2人中含有醉酒驾车司机的概率.
某市 四所中学报名参加某高校今年自主招生的学生人数如下表所示:
四所中学报名参加某高校今年自主招生的学生人数如下表所示:
| 中学 |  |  | 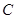 | 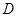 |
| 人数 | 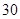 | 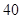 | 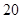 | 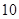 |
(1)问
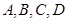 四所中学各抽取多少名学生?
四所中学各抽取多少名学生?(2)从参加问卷调查的
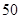 名学生中随机抽取两名学生,求这两名学生自同一所中学的概率;
名学生中随机抽取两名学生,求这两名学生自同一所中学的概率;(3)在参加问卷调查的
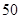 名学生中,从自
名学生中,从自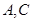 两所中学的学生当中随机抽取两名学
两所中学的学生当中随机抽取两名学生,用
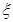 表示抽得
表示抽得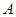 中学的学生人数,求
中学的学生人数,求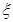 的分布列和期望.
的分布列和期望. 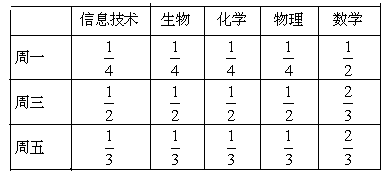
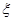 ,求随机变量
,求随机变量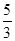 ,D(η)=
,D(η)=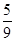 ,求a∶b∶c.
,求a∶b∶c.