题目内容
已知椭圆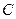 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在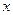 轴上,离心率为
轴上,离心率为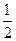 ,椭圆
,椭圆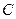 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为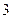 .
.
(1)求椭圆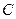 的标准方程;
的标准方程;
(2)若过点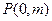 的直线
的直线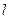 与椭圆
与椭圆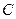 交于不同的两点
交于不同的两点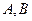 ,且
,且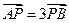 ,求实数
,求实数 的取值范围.
的取值范围.
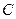 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在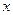 轴上,离心率为
轴上,离心率为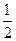 ,椭圆
,椭圆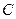 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为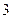 .
.(1)求椭圆
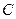 的标准方程;
的标准方程;(2)若过点
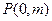 的直线
的直线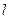 与椭圆
与椭圆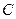 交于不同的两点
交于不同的两点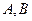 ,且
,且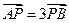 ,求实数
,求实数 的取值范围.
的取值范围.(1)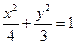
(2)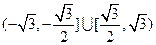
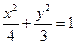
(2)
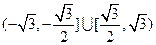
(1)设所求的椭圆方程为: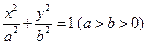
由题意: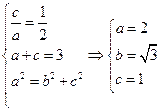
所求椭圆方程为: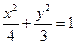 .
.
(2)若过点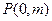 的斜率不存在,则
的斜率不存在,则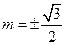 .
.
若过点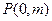 的直线斜率为
的直线斜率为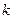 ,即:
,即: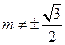 时,
时,
直线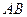 的方程为
的方程为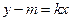
由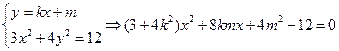
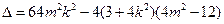
因为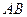 和椭圆
和椭圆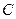 交于不同两点
交于不同两点
所以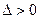 ,
,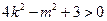
所以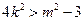 ①
①
设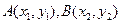
由已知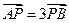 ,则
,则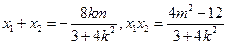 ②
②
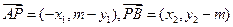
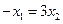 ③
③
将③代入②得: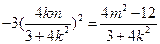
整理得: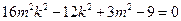
所以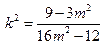 代入①式得
代入①式得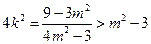
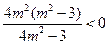 ,解得
,解得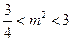 .
.
所以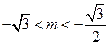 或
或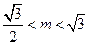 .
.
综上可得,实数 的取值范围为:
的取值范围为: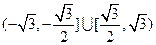 .
.
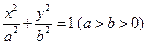
由题意:
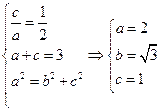
所求椭圆方程为:
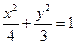 .
.(2)若过点
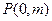 的斜率不存在,则
的斜率不存在,则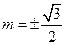 .
.若过点
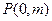 的直线斜率为
的直线斜率为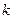 ,即:
,即: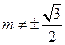 时,
时,直线
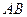 的方程为
的方程为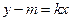
由
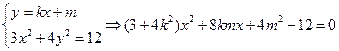
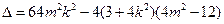
因为
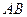 和椭圆
和椭圆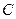 交于不同两点
交于不同两点所以
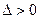 ,
,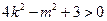
所以
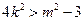 ①
①设
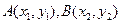
由已知
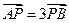 ,则
,则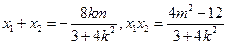 ②
②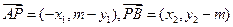
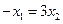 ③
③将③代入②得:
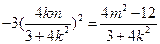
整理得:
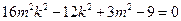
所以
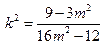 代入①式得
代入①式得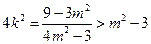
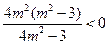 ,解得
,解得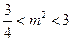 .
.所以
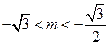 或
或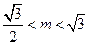 .
.综上可得,实数
 的取值范围为:
的取值范围为: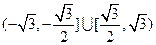 .
.
练习册系列答案
相关题目
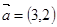 表示出来的是( )
表示出来的是( )



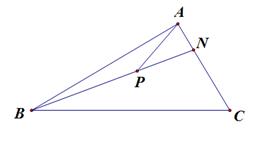
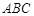 中,
中, 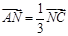 ,
,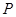 是
是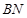 上的一点,若
上的一点,若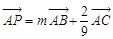 ,则实数
,则实数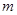 的值为( )
的值为( ) 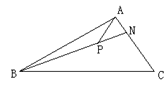




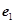 ,
, 是平面内的一组基底,则下列四组向量不能作为平面向量的基底的是( )
是平面内的一组基底,则下列四组向量不能作为平面向量的基底的是( ) ,且
,且 ∥
∥ ,则
,则 的值是( )
的值是( )


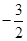
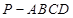 中,底面
中,底面 是平行四边形,
是平行四边形,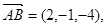
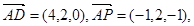 则直线
则直线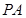 与底面
与底面




 中,
中, ,
, ,
, ,则
,则 ( )(用
( )(用 ,
, 表示)
表示)



