椭圆的方程为+＝1.A1.A2分别是椭圆的左.右顶点.P是椭圆上任一点.作A1Q⊥A1P.A2Q⊥A2P.设A1Q与A2Q相交于点Q.求Q点的轨迹方程．题目和参考答案——青夏教育精英家教网——

题目内容

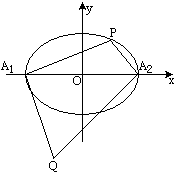
椭圆的方程为＋＝1，A₁、A₂分别是椭圆的左、右顶点，P是椭圆上任一点，作A₁Q⊥A₁P，A₂Q⊥A₂P，设A₁Q与A₂Q相交于点Q，求Q点的轨迹方程．

答案：
解析：

　　解：如图所示，设Q(x，y)，P(x₁，y₁)，

　　则＋＝1，

　　k_PA1＝，

　　k_PA2＝．

　　∵A₁Q⊥A₁P，A₂Q⊥A₂P．

　　∴A₁Q：y＝－(x＋a)，　　①．

　　A₂Q：y＝－(x－a)．　　　②

　　①×②得y₂＝(x²－a²)，

　　即y²＝－(x²－a²)，得＋＝1．

　　这就是Q点的轨迹方程．

　　分析：因Q点随P点的运动而运动，而P点在已知椭圆上，故可用转移法求解．

　　点评：本题亦可用椭圆参数方程，即设P点的坐标为(acos，bsin)，建立A₁Q、A₂Q的方程，求得Q的轨迹方程．解题时不宜求出交点再消参数，否则消参不易．

练习册系列答案

第一课堂课堂作业系列答案

金牌堂堂练系列答案

一本搞定系列答案

同步学典一课多练系列答案

名师金典BFB初中课时优化系列答案

经典密卷系列答案

启智课堂系列答案

金牌课堂练系列答案

优等生全优计划系列答案

新课堂作业本系列答案

相关题目

已知椭圆的方程为＋＝1，焦点在x轴上，则m的取值范围是

－4≤m≤4

－4＜m＜4且m≠0

m＞4或m＜－4

0＜m＜4

把一颗骰子投掷两次，记第一次出现的点数为a²，第二次出现的点数为b²(其中a＞0，b＞0)．

(Ⅰ)若记事件A“焦点在x轴上的椭圆的方程为＋＝1”，求事件A的概率；

(Ⅱ)若记事件B“离心率为2的双曲线的方程为－＝1”，求事件B的概率．

设椭圆的方程为＋＝1(m、n＞0)，过原点且倾角为θ和π－θ(0＜θ＜)的两条直线分别交椭圆于A、C和B、D两点．

(1)

用θ、m、n表示四边形ABCD的面积S

(2)

若m、n为定值，当θ在(0，］上变化时，求S的最大值u

(3)

如果u＞mn，求的取值范围

已知椭圆C₁的方程为＋＝1(a＞b＞0)，离心率为，两个焦点分别为F₁和F₂，椭圆C₁上一点到F₁和F₂的距离之和为12.椭圆C₂的方程为＋＝1.圆C_k：x²＋y²＋2kx－4y－21＝0(k∈R)的圆心为点A_k.

(1)求椭圆C₁的方程；

(2)求△A_kF₁F₂的面积；

(3)若点P为椭圆C₂上的动点，点M为过点P且垂直于x轴的直线上的点，＝e(e为椭圆C₂的离心率)，求点M的轨迹．