题目内容
【题目】设
（1）试讨论f(x)在
上的单调性；
（2）令g（x）=ax-a（a<1）当m=-1时，若恰有两个整数x1，x2，使得
求实数a的最小值.
【答案】（1）见解析（2）
【解析】试题分析：（1）先求导数，再讨论导函数零点，根据导函数符号确定单调性，（2）先分别讨论函数
图像，根据图像关系确定整数解，结合整数解列不等关系，求a的取值范围，即得最小值.
试题解析：（（Ⅰ）
.
令
，则
.
若
，即
时，
，此时
在
上单调递增.
若
，即
时，此时在
上单调递减，在
上单调递增.
（Ⅱ）
就是
利用导数知识确定
的图象：
在
内单减，在
内单增，
是极小值点，且
.
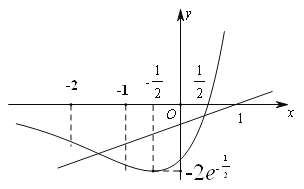
直线g(x)=ax-a过定点(1,0),a＞0.
存在的两个整数点是0,-1.
于是
，所以
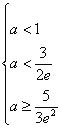，解得
故
的最小值是
【题目】随着电商的快速发展，快递业突飞猛进，到目前，中国拥有世界上最大的快递市场.某快递公司收取快递费用的标准是：重量不超过
的包裹收费10元；重量超过的包裹，除收费10元之外，每超过（不足，按计算）需再收5元.
该公司将最近承揽的100件包裹的重量统计如下：
包裹重量（单位： | 1 | 2 | 3 | 4 | 5 |
包裹件数 | 43 | 30 | 15 | 8 | 4 |
公司对近60天，每天揽件数量统计如下表：
包裹件数范围 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
包裹件数（近似处理） | 50 | 150 | 250 | 350 | 450 |
天数 | 6 | 6 | 30 | 12 | 6 |
以上数据已做近似处理，并将频率视为概率.
（1）计算该公司未来5天内恰有2天揽件数在101~300之间的概率；
（2）①估计该公司对每件包裹收取的快递费的平均值；
②根据以往的经验，公司将快递费的三分之一作为前台工作人员的工资和公司利润，剩余的用作其他费用.目前前台有工作人员3人，每人每件揽件不超过150件，日工资100元.公司正在考虑是否将前台工作人员裁减1人，试计算裁员前后公司每日利润的数学期望，若你是公司老总，是否进行裁减工作人员1人？
【题目】某学校在九年级上学期开始时要掌握全年级学生每分钟跳绳的情况，随机抽取了100名学生进行测试，得到频率分布直方图（如图），且规定计分规则如下表：
每分钟跳绳个数 |
|
|
|
|
得分 | 17 | 18 | 19 | 20 |
（1）请估计学生的跳绳个数的众数和平均数（保留整数）；
（2）若从跳绳个数在
，
两组中按分层抽样的方法抽取9人参加正式测试，并从中任意选取2人，求2人得分之和不大于34分的概率.
