题目内容
【题目】若直角坐标平面内的两点P,Q满足条件:①P,Q都在函数![]() 的图像上;②P,Q关于原点对称,则称P,Q是函数
的图像上;②P,Q关于原点对称,则称P,Q是函数![]() 的一对“友好点对”(点对P,Q与Q,P看作同一对“友好点对”).已知函数
的一对“友好点对”(点对P,Q与Q,P看作同一对“友好点对”).已知函数 若此函数的“友好点对”有且只有一对,则a的取值范围是( )
若此函数的“友好点对”有且只有一对,则a的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】A
【解析】
根据原点对称的性质,求出当﹣4≤x<0时函数关于原点对称的函数,条件转化函数f(x)=logax,(x>0)与y=﹣|x﹣3|,(0<x≤4),只有一个交点,作出两个函数的图象,利用数形结合结合对数函数的性质进行求解即可.
当﹣4≤x<0时,函数y=|x+3|关于原点对称的函数为﹣y=|﹣x+3|,即y=﹣|x﹣3|,(0<x≤4),
若此函数的“友好点对”有且只有一对,
则等价为函数f(x)=logax,(x>0)与y=﹣|x﹣3|,(0<x≤4),只有一个交点,
作出两个函数的图象如图:
若a>1,则f(x)=logax,(x>0)与y=﹣|x﹣3|,(0<x≤4),只有一个交点,满足条件,
当x=4时,y=﹣|4﹣3|=﹣1,
若0<a<1,要使两个函数只有一个交点,
则满足f(4)<﹣1,
即loga4<﹣1,得![]() a<1,
a<1,
综上![]() a<1或a>1,
a<1或a>1,
即实数a的取值范围是![]() ,
,
故选:A.
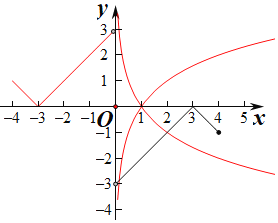

练习册系列答案
相关题目