题目内容
8.已知f(x)是R上的奇函数,且x>0时,f(x)=x2-x-1,求f(x)解析式.分析 直接利用函数的奇偶性求解函数的解析式即可.
解答 解:因为函数是奇函数,可得f(x)=-f(-x),f(0)=0.
x<0时,-x>0,x>0时,f(x)=x2-x-1,
∴f(x)=-f(-x)=-(-x)2+x+1=-x2+x+1.
f(x)=$\left\{\begin{array}{l}{x}^{2}-x-1,x>0\\ 0,x=0\\-{x}^{2}+x+1,x<0\end{array}\right.$.
点评 本题考查函数的解析式求法,考查计算能力.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
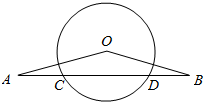 已知:如图△OAB为等腰三角形,底边AB角⊙O于点C,D,求证:AC=BD.
已知:如图△OAB为等腰三角形,底边AB角⊙O于点C,D,求证:AC=BD. 如图正方体ABCD-A1B1C1D1中,下列结论中正确的序号是①③.
如图正方体ABCD-A1B1C1D1中,下列结论中正确的序号是①③.