题目内容
(2012•太原模拟)某高中社团进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查分别得到如图1
所示统计表和如图2所示各年龄段人数频率分布直方图:

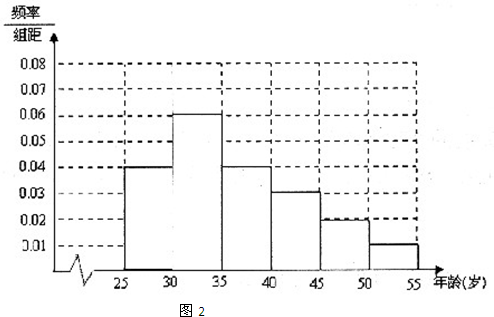
请完成以下问题:
(1)补全频率直方图,并求n,a,p的值
(2)从[40,45)岁和[45,50)岁年龄段的“时尚族”中采用分层抽样法抽取6人参加网络时尚达人大赛,其中选取2人作为领队,求选取的2名领队中年龄在[40,45)岁的概率.
所示统计表和如图2所示各年龄段人数频率分布直方图:


请完成以下问题:
(1)补全频率直方图,并求n,a,p的值
(2)从[40,45)岁和[45,50)岁年龄段的“时尚族”中采用分层抽样法抽取6人参加网络时尚达人大赛,其中选取2人作为领队,求选取的2名领队中年龄在[40,45)岁的概率.
分析:(1)根据题意,由频率分步直方图的意义可得第二组的频率,进而可得其对应长方形的高,据此可以补全直方图,结合分布表,计算可得n、a、p的值;
(2)先有分层抽样方法可得各个年龄段的人数,设a1、a2、a3、a4为[40,45)岁中抽得的4人,b1、b2为[45,50)岁中抽得的2人,进而用列举法可得抽出2人的全部情况,由古典概型公式计算可得答案.
(2)先有分层抽样方法可得各个年龄段的人数,设a1、a2、a3、a4为[40,45)岁中抽得的4人,b1、b2为[45,50)岁中抽得的2人,进而用列举法可得抽出2人的全部情况,由古典概型公式计算可得答案.
解答:解(1)第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,
所以高为
=0.06.频率直方图如下:
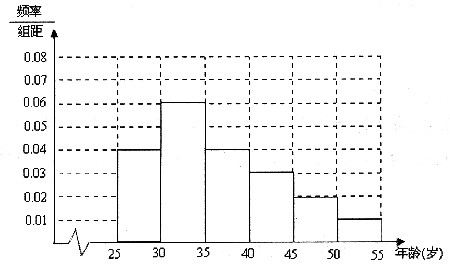
第一组的人数为
=200,频率为0.04×5=0.2,所以n=
=1000,
所以第二组的人数为1000×0.3=300,p=
=0.65,
四组的频率为 0.03×5=0.15,第四组的人数为1000×0.15=150,
所以a=150×0.4=60.
(2)因为[40,45)岁与[45,50)岁年龄段的“时尚族”的比值为60:30=2:1,
所以采用分层抽样法抽取6人,[40,45)岁中有4人,[45,50)岁中有2人.
设a1、a2、a3、a4为[40,45)岁中抽得的4人,b1、b2为[45,50)岁中抽得的2人,
全部可能的结果有:
(a1,a2),( a1,a3),( a1,a4),( a1,b1),( a1,b2),(a2,a3),(a2,a4),(a2,b1),(a2,b2),(a3,a4),(a3,b1),(a3,b2),(a4,b1),(a4,b2),(b1,b2),共15个,
所以所求概率为
=
.
所以高为
| 0.3 |
| 5 |

第一组的人数为
| 120 |
| 0.6 |
| 200 |
| 0.2 |
所以第二组的人数为1000×0.3=300,p=
| 195 |
| 300 |
四组的频率为 0.03×5=0.15,第四组的人数为1000×0.15=150,
所以a=150×0.4=60.
(2)因为[40,45)岁与[45,50)岁年龄段的“时尚族”的比值为60:30=2:1,
所以采用分层抽样法抽取6人,[40,45)岁中有4人,[45,50)岁中有2人.
设a1、a2、a3、a4为[40,45)岁中抽得的4人,b1、b2为[45,50)岁中抽得的2人,
全部可能的结果有:
(a1,a2),( a1,a3),( a1,a4),( a1,b1),( a1,b2),(a2,a3),(a2,a4),(a2,b1),(a2,b2),(a3,a4),(a3,b1),(a3,b2),(a4,b1),(a4,b2),(b1,b2),共15个,
所以所求概率为
| 6 |
| 15 |
| 2 |
| 5 |
点评:本题考查频率分步直方图的画法、应用以及列举法求古典概型,关键是掌握频率分步直方图意义以及运算、

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
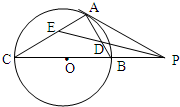 (2012•太原模拟)选修4-1:几何证明选讲
(2012•太原模拟)选修4-1:几何证明选讲