题目内容
（2012•太原模拟）已知函数f（x）=2x+x，g（x）=log2x+x，h（x）=log4x+x的零点依次为a，b，c，则（ ）
分析：先把所求问题转化为直线y=-x与函数y=2x，y=log2x，y=log4x的交点；再同一直角坐标系中画出图象，结合图象即可得到结论．
解答：解：因为函数f（x）=2x+x，g（x）=log2x+x，h（x）=log4x+x的零点可以转化为直线y=-x
与函数y=2x，y=log2x，y=log4x的交点；
如图：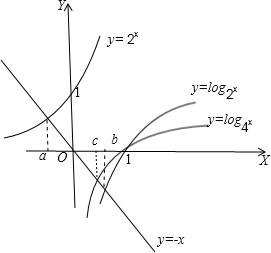
由图得：a＜c＜b．
故选：C．
与函数y=2x，y=log2x，y=log4x的交点；
如图：
由图得：a＜c＜b．
故选：C．
点评：本题考查函数的零点有数形结合的数学思想方法，数形结合是数学解题中常用的思想方法，能够变抽象思维为形象思维，有助于把握数学问题的本质．
练习册系列答案
相关题目
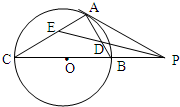（2012•太原模拟）选修4-1：几何证明选讲