题目内容
已知函数f(x)=ax2-(a+3)x+4,(1)若y=f(x)的两个零点为α,β,且满足0<α<2<β<4,求实数a的取值范围;
(2)若函数y=loga+1f(x)存在最值,求实数a的取值范围,并指出最值是最大值还是最小值.
分析:(1)画出对应图象,由图象得出的结论可以求出实数a的取值范围;
(2)先求真数的最值,再利用复合函数的最值求法求整个函数的最值即可,(注意底数满足的条件).
(2)先求真数的最值,再利用复合函数的最值求法求整个函数的最值即可,(注意底数满足的条件).
解答: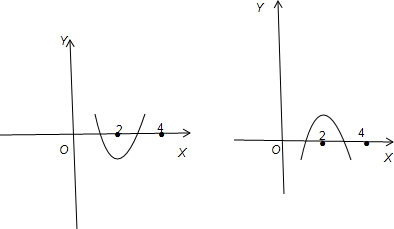 解:(1)满足条件的图形如下,
解:(1)满足条件的图形如下,
所以有
或
?
<a<1
故所求实数a的取值范围是 (
,1);
(2)因为f(x)=a(x-
)2+4-
.有最值为4-
,
当4-
>0时,
可得,a<0或1<a<9,又a+1>0?a>-1.
由复合函数的最值可得
当-1<a<0时,y=loga+1)f(x)存在最小值
当1<a<9时,y=loga+1)f(x)存在最小值.
故-1<a<0或1<a<9时,y=loga+1)f(x)存在最小值.
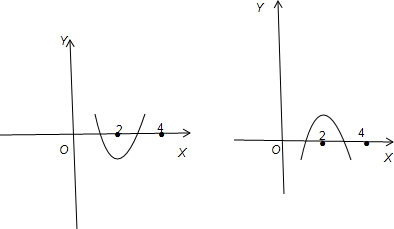 解:(1)满足条件的图形如下,
解:(1)满足条件的图形如下,所以有
|
|
?
| 2 |
| 3 |
故所求实数a的取值范围是 (
| 2 |
| 3 |
(2)因为f(x)=a(x-
| a+3 |
| 2a |
| (a+3)2 |
| 4a |
| (a+3)2 |
| 4a |
当4-
| (a+3)2 |
| 4a |
可得,a<0或1<a<9,又a+1>0?a>-1.
由复合函数的最值可得
当-1<a<0时,y=loga+1)f(x)存在最小值
当1<a<9时,y=loga+1)f(x)存在最小值.
故-1<a<0或1<a<9时,y=loga+1)f(x)存在最小值.
点评:本题涉及到一元二次方程的根的分布与系数的关系以及函数最值的应用,是对基础知识的综合考查.

练习册系列答案
相关题目