题目内容
(本题满分8分)已知 ,函数
,函数 .
.
(Ⅰ)求 的极值(用含
的极值(用含 的式子表示);
的式子表示);
(Ⅱ)若 的图象与
的图象与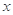 轴有3个不同交点,求
轴有3个不同交点,求 的取值范围.
的取值范围.
【答案】
(Ⅰ)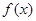 的极大值
的极大值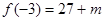 ,极小值为
,极小值为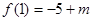 (Ⅱ)
(Ⅱ)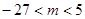
【解析】
试题分析:(Ⅰ)令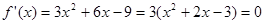 ,得:
,得: 或-3.
或-3.
当 或
或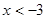 时,
时,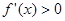 ;
;
当 时,
时,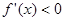 ;
;
故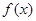 在区间
在区间 ,
, 单调递增;在区间
单调递增;在区间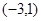 单调递减 3’
单调递减 3’
于是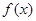 的极大值
的极大值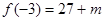 ,极小值为
,极小值为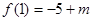 1’
1’
(Ⅱ)令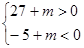 ,
3’
,
3’
得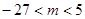 1’
1’
考点:本题考查了极值点求法及单调性的运用
点评:求可导函数的极值的基本步骤为:①求导函数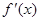 ;②求方程
;②求方程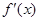 =0的根;③检查
=0的根;③检查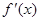 在方程根左右的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值.
在方程根左右的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值.

练习册系列答案
相关题目

 是常数),且
是常数),且 (
( 为坐标原点).
为坐标原点). 的单调递增区间;
的单调递增区间; 时,
时, 的最大值为4,求
的最大值为4,求 的值;
的值; 。
。 的振幅和最小正周期;
的振幅和最小正周期; 时,函数
时,函数 时,求
时,求 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,
, ,且
,且
 与
与 共线,求
共线,求 .
. 的大致图象;
的大致图象;
 的零点.
的零点.