题目内容
椭圆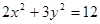 的两焦点之间的距离为
的两焦点之间的距离为
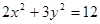 的两焦点之间的距离为
的两焦点之间的距离为A.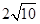 | B.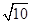 | C.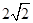 | D.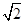 |
C
试题分析:根据题意,由于椭圆的方程为
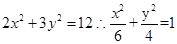 ,故可知长半轴的长为
,故可知长半轴的长为 ,那么可知两个焦点 的坐标为
,那么可知两个焦点 的坐标为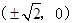 ,因此可知两焦点之间的距离为
,因此可知两焦点之间的距离为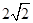 ,故选C
,故选C点评:解决的关键是将方程变为标准式,然后结合性质得到结论,属于基础题。

练习册系列答案
相关题目
题目内容
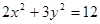 的两焦点之间的距离为
的两焦点之间的距离为A.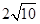 | B.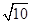 | C.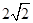 | D.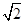 |
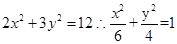 ,故可知长半轴的长为
,故可知长半轴的长为 ,那么可知两个焦点 的坐标为
,那么可知两个焦点 的坐标为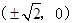 ,因此可知两焦点之间的距离为
,因此可知两焦点之间的距离为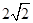 ,故选C
,故选C