题目内容
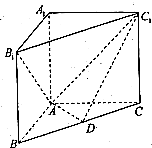 三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=2a,AA1=t•a(t>0,t∈R),∠BAC=120°,
三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=2a,AA1=t•a(t>0,t∈R),∠BAC=120°,(1)若在BC上存在点D,使DA1⊥平面AB1C1,求实数t的值,并判断D点的位置;
(2)在(1)成立的条件下,求二面角D-AC1-B1大小的余弦值.
分析:(1)可考虑用空间向量来解决立体几何问题,若DA1⊥平面AB1C1,则
垂直于平面AB1C1上两个不共线向量.
先建立空间直角坐标系,把定点坐标表示出来,求出向量
的坐标,在平面AB1C1上,找两个不共线的向量,求出坐标,再计算这两个向量与
的数量积,让数量积等于0,求D点坐标,若能求出,则ED点存在,否则,不存在.
(2)求二面角的大小,只需求这两个平面的法向量夹角的大小,法向量的夹角,是这两个平面所成角,或所成角的补角.
| A1D |
先建立空间直角坐标系,把定点坐标表示出来,求出向量
| A1D |
| A1D |
(2)求二面角的大小,只需求这两个平面的法向量夹角的大小,法向量的夹角,是这两个平面所成角,或所成角的补角.
解答:解:(1)以A为原点,AB所在直线为x轴,AC所在直线为y轴,Aa1所在直线为z轴,建立空间直角坐标系,则
A(0,0,0),B(
a,-a,0)C(0,2a,0),A1(0,0,ta),B1(
a,-a,ta),C1(0,2a,ta)
令
=λ
,D(x,y,z),∴(x-
a,y+a,z)=λ(0-
a,2a+a,0)
∴
,∴D(-
aλ+
a,3aλ-a,0)
=(-
aλ+
a,3aλ-a,-ta),
=(
a,-a,ta),
=(0,2a,ta)
∴t=1,λ=
,D是BC的中点.
(2)平面DAC1的法向量为
=(1,-
,2
),平面DAC1的法向量为
=(
,1,-2)
cos<
,
>=
=
,∴二面角D-AC1-B1大小的余弦值w为
.
A(0,0,0),B(
| 3 |
| 3 |
令
| BD |
| BC |
| 3 |
| 3 |
∴
|
| 3 |
| 3 |
| A1D |
| 3 |
| 3 |
| AB1 |
| 3 |
| AC1 |
|
∴t=1,λ=
| 1 |
| 2 |
(2)平面DAC1的法向量为
| n |
| 3 |
| 3 |
| m |
| 3 |
cos<
| n |
| m |
| ||||
|
|
| ||
| 4 |
| ||
| 4 |
点评:本题考查了利用空间向量证明线面垂直,以及求二面角的大小的问题,属于空间向量的应用.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=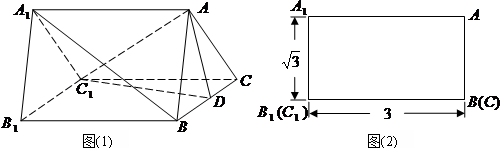
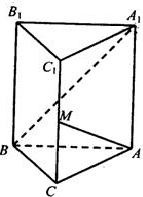 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1, 如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.
如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.