题目内容
设集合W是满足下列两个条件的无穷数列 的集合:①对任意
的集合:①对任意 ,
, 恒成立;②对任意
恒成立;②对任意 ,存在与n无关的常数M,使
,存在与n无关的常数M,使 恒成立.
恒成立.
(1)若 是等差数列,
是等差数列, 是其前n项和,且
是其前n项和,且 试探究数列
试探究数列 与集合W之间的关系;
与集合W之间的关系;
(2)设数列 的通项公式为
的通项公式为 ,且
,且 ,求M的取值范围.
,求M的取值范围.
【答案】
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)先根据条件,利用等差数列的性质得到 的前n项和
的前n项和 ,然后检验其是否满足①②条件即可;(2)由数列
,然后检验其是否满足①②条件即可;(2)由数列 的通项公式经作差可知,当
的通项公式经作差可知,当 时,
时, ,此时,数列
,此时,数列 单调递减,当
单调递减,当 时,
时,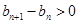 ,即
,即 ,从而得到数列
,从而得到数列 中的最大项为
中的最大项为 ,由
,由 恒成立,从而知
恒成立,从而知 的取值范围是
的取值范围是 .
.
试题解析:(1)设等差数列 的公差是
的公差是 ,则
,则
 解得
解得 1分
1分
∴ (3分)
(3分)
∴
∴ ,适合条件①
,适合条件①
又 ,
,
∴当 或
或 时,
时, 取得最大值20,即
取得最大值20,即 ,适合条件②.
,适合条件②.
综上, (6分)
(6分)
(2)∵ ,
,
∴当 时,
时, ,此时,数列
,此时,数列 单调递减; 9分
单调递减; 9分
当 时,
时,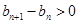 ,即
,即 , 10分
, 10分
因此,数列 中的最大项是
中的最大项是 , 11分
, 11分
∴ ,即M的取值范围是
,即M的取值范围是 . 12分
. 12分
考点:1.新概念的理解;2.等差数列的性质;3.数列的单调性.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目