题目内容
【题目】设函数f(x)为定义在R奇函数,当x>0时,f(x)=﹣2x2+4x+1,
(1)求:当x<0时,f(x)的表达式;
(2)用分段函数写出f(x)的表达式;
(3)若函数h(x)=f(x)﹣a恰有三个零点,求a的取值范围(只要求写出结果).
【答案】
(1)解:设x<0,则﹣x>0,
∵当x>0时,f(x)=﹣2x2+4x+1,
∴f(﹣x)=﹣2x2﹣4x+1,
∵f(x)为定义在R上是奇函数,
∴f(x)=﹣f(﹣x)=2x2+4x﹣1
(2)解:∵f(x)为定义在R上是奇函数,
∴f(0)=﹣f(﹣0),则f(0)=0,
由(1)可得,f(x)= 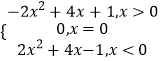
(3)解:由函数h(x)=f(x)﹣a=0得,f(x)=a,
由条件得,当x>0时,
f(x)=﹣2x2+4x+1=﹣2(x﹣1)2+3,
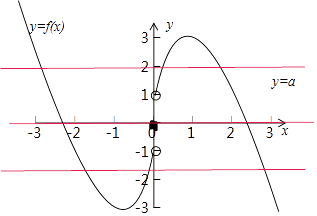
由(2)画出函数f(x)和y=a的图象,如图所示:
∵函数h(x)=f(x)﹣a恰有三个零点,
∴由图得,﹣3<a<﹣1或a=0或1<a<3,
∴a的取值范围是
{a|﹣3<a<﹣1或a=0或1<a<3}
【解析】(1)设x<0则﹣x>0,根据题意和奇函数的性质求出当x<0时,f(x)的表达式;(2)由奇函数的性质求出f(0)=0,由(1)和分段函数表示出f(x);(3)利用配方法化简x>0时的f(x),由(2)和二次函数的图象画出f(x)的图象,根据函数零点的几何意义和图象,求出满足题意的a的取值范围.
【考点精析】根据题目的已知条件,利用函数奇偶性的性质的相关知识可以得到问题的答案,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目